Question
Solve the equation
x=22π2logπ(50)+22logπ(50)
Alternative Form
x≈4.950538
Evaluate
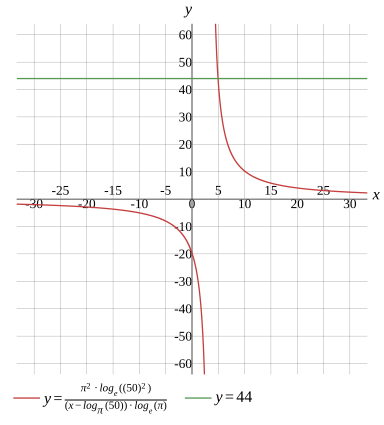
(x−logπ(50))×ln(π)π2ln(502)=44
Find the domain
More Steps


Evaluate
(x−logπ(50))×ln(π)=0
Multiply the terms
ln(π)×(x−logπ(50))=0
Rewrite the expression
x−logπ(50)=0
Move the constant to the right side
x=0+logπ(50)
Removing 0 doesn't change the value,so remove it from the expression
x=logπ(50)
(x−logπ(50))×ln(π)π2ln(502)=44,x=logπ(50)
Simplify
More Steps


Evaluate
(x−logπ(50))×ln(π)π2ln(502)
Simplify
(x−logπ(50))×ln(π)π2×2ln(50)
Use the commutative property to reorder the terms
(x−logπ(50))×ln(π)2π2ln(50)
Multiply the terms
ln(π)×(x−logπ(50))2π2ln(50)
ln(π)×(x−logπ(50))2π2ln(50)=44
Cross multiply
2π2ln(50)=ln(π)×(x−logπ(50))×44
Simplify the equation
2π2ln(50)=44ln(π)×(x−logπ(50))
Rewrite the expression
2π2ln(50)=2×22ln(π)×(x−logπ(50))
Evaluate
π2ln(50)=22ln(π)×(x−logπ(50))
Swap the sides of the equation
22ln(π)×(x−logπ(50))=π2ln(50)
Divide both sides
22ln(π)22ln(π)×(x−logπ(50))=22ln(π)π2ln(50)
Divide the numbers
x−logπ(50)=22ln(π)π2ln(50)
Divide the numbers
x−logπ(50)=22π2logπ(50)
Move the constant to the right side
x=22π2logπ(50)+logπ(50)
Simplify
x=22logπ(50)×(π2+22)
Multiply the numbers
x=22π2logπ(50)+22logπ(50)
Check if the solution is in the defined range
x=22π2logπ(50)+22logπ(50),x=logπ(50)
Solution
x=22π2logπ(50)+22logπ(50)
Alternative Form
x≈4.950538
Show Solution

Graph