Question
Solve the equation
θ=⎩⎨⎧−arccos(31)+2kπkπarccos(31)+2kπ,k∈Z
Alternative Form
θ≈⎩⎨⎧−70.528779∘+360∘k180∘k70.528779∘+360∘k,k∈Z
Alternative Form
θ≈⎩⎨⎧−1.230959+2kπkπ1.230959+2kπ,k∈Z
Evaluate
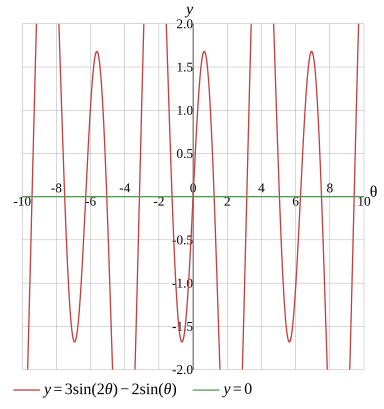
3sin(2θ)−2sin(θ)=0
Rewrite the expression
3×2sin(θ)cos(θ)−2sin(θ)=0
Simplify
6sin(θ)cos(θ)−2sin(θ)=0
Factor the expression
More Steps


Calculate
6sin(θ)cos(θ)−2sin(θ)
Factor out 2 from the expression
2(3sin(θ)cos(θ)−sin(θ))
Factor the expression
More Steps


Calculate
3sin(θ)cos(θ)−sin(θ)
Rewrite the expression
sin(θ)×3cos(θ)−sin(θ)
Factor out sin(θ) from the expression
sin(θ)(3cos(θ)−1)
2sin(θ)(3cos(θ)−1)
2sin(θ)(3cos(θ)−1)=0
Elimination the left coefficient
sin(θ)(3cos(θ)−1)=0
Separate the equation into 2 possible cases
sin(θ)=03cos(θ)−1=0
Solve the equation
More Steps


Evaluate
sin(θ)=0
Use the inverse trigonometric function
θ=arcsin(0)
Calculate
θ=0
Add the period of kπ,k∈Z to find all solutions
θ=kπ,k∈Z
θ=kπ,k∈Z3cos(θ)−1=0
Solve the equation
More Steps


Evaluate
3cos(θ)−1=0
Move the constant to the right-hand side and change its sign
3cos(θ)=0+1
Removing 0 doesn't change the value,so remove it from the expression
3cos(θ)=1
Divide both sides
33cos(θ)=31
Divide the numbers
cos(θ)=31
Use the inverse trigonometric function
θ=arccos(31)
Calculate
θ=−arccos(31)θ=arccos(31)
Add the period of 2kπ,k∈Z to find all solutions
θ=−arccos(31)+2kπ,k∈Zθ=arccos(31)+2kπ,k∈Z
Find the union
θ={−arccos(31)+2kπarccos(31)+2kπ,k∈Z
θ=kπ,k∈Zθ={−arccos(31)+2kπarccos(31)+2kπ,k∈Z
Solution
θ=⎩⎨⎧−arccos(31)+2kπkπarccos(31)+2kπ,k∈Z
Alternative Form
θ≈⎩⎨⎧−70.528779∘+360∘k180∘k70.528779∘+360∘k,k∈Z
Alternative Form
θ≈⎩⎨⎧−1.230959+2kπkπ1.230959+2kπ,k∈Z
Show Solution

Rewrite the equation
−8y2x2+y4=0
Evaluate
3sin(2θ)−2sin(θ)=0
Simplify the expression
6sin(θ)cos(θ)−2sin(θ)=0
Multiply both sides
6sin(θ)cos(θ)×r2−2sin(θ)×r2=0
Use substitution
More Steps


Evaluate
6sin(θ)cos(θ)×r2−2sin(θ)×r2
Use substitution
More Steps


Evaluate
6sin(θ)cos(θ)×r2
Use the commutative property to reorder the terms
r2sin(θ)cos(θ)×6
To covert the equation to rectangular coordinates using conversion formulas,substitute rsinθ for y
rcos(θ)×y×6
To covert the equation to rectangular coordinates using conversion formulas,substitute rcosθ for x
yx×6
Multiply the terms
6yx
6yx−2sin(θ)×r2
Use substitution
More Steps


Evaluate
−2sin(θ)×r2
Use the commutative property to reorder the terms
r2sin(θ)(−2)
To covert the equation to rectangular coordinates using conversion formulas,substitute rsinθ for y
ry(−2)
Evaluate
yr(−2)
Multiply the terms
−2yr
6yx−2yr
6yx−2yr=0
Simplify the expression
−2yr=−6yx
Square both sides of the equation
(−2yr)2=(−6yx)2
Evaluate
(−2y)2r2=(−6yx)2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
(−2y)2(x2+y2)=(−6yx)2
Use substitution
4y2(x2+y2)=(−6yx)2
Evaluate the power
4y2(x2+y2)=36y2x2
Divide both sides of the equation by 4
y2(x2+y2)=9y2x2
Calculate
y2x2+y4=9y2x2
Move the expression to the left side
y2x2+y4−9y2x2=0
Solution
More Steps


Evaluate
y2x2−9y2x2
Collect like terms by calculating the sum or difference of their coefficients
(1−9)y2x2
Subtract the numbers
−8y2x2
−8y2x2+y4=0
Show Solution

Graph