Solve log_{5}(2x^2 - 8x 7) = 2 \log_{5}x

Evaluate

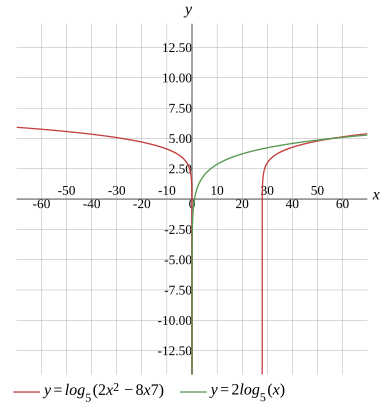
lo g_{5} (2 x^{2} - 8 x \times 7) = 2 lo g_{5} (x)

Find the domain

More Steps

lo g_{5} (2 x^{2} - 8 x \times 7) = 2 lo g_{5} (x), x > 28

Multiply the terms

lo g_{5} (2 x^{2} - 56 x) = 2 lo g_{5} (x)

Move the expression to the left side

lo g_{5} (2 x^{2} - 56 x) - 2 lo g_{5} (x) = 0

Add the terms

More Steps

lo g_{5} (\frac{2 x - 56}{x}) = 0

Convert the logarithm into exponential form using the fact that lo g_{a} x = b is equal to x = a^{b}

\frac{2 x - 56}{x} = 5^{0}

Evaluate the power

\frac{2 x - 56}{x} = 1

Cross multiply

2 x - 56 = x

Move the variable to the left side

2 x - 56 - x = 0

Subtract the terms

More Steps

x - 56 = 0

Move the constant to the right side

x = 0 + 56

Removing 0 doesn't change the value,so remove it from the expression

x = 56

Check if the solution is in the defined range

x = 56, x > 28

Solution

x = 56

Solve the equation