Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
θ∈/R
Alternative Form
No real solution
Evaluate
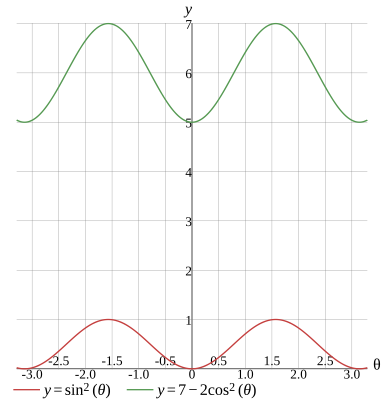
sin2(θ)=7−2cos2(θ)
Use sin2(x)=1−cos2(x) to rewrite the expression
1−cos2(θ)=7−2cos2(θ)
Move the expression to the left side
1−cos2(θ)−(7−2cos2(θ))=0
Calculate
More Steps
Evaluate
1−cos2(θ)−(7−2cos2(θ))
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
1−cos2(θ)−7+2cos2(θ)
Subtract the numbers
−6−cos2(θ)+2cos2(θ)
Add the terms
More Steps
Evaluate
−cos2(θ)+2cos2(θ)
Factor the expression
(−1+2)cos2(θ)
Add the numbers
1×cos2(θ)
Calculate
cos2(θ)
−6+cos2(θ)
−6+cos2(θ)=0
Add or subtract both sides
cos2(θ)=0+6
Removing 0 doesn't change the value,so remove it from the expression
cos2(θ)=6
Take the root of both sides of the equation and remember to use both positive and negative roots
cos(θ)=±6
Separate the equation into 2 possible cases
cos(θ)=6cos(θ)=−6
Calculate
More Steps
Evaluate
cos(θ)=6
Use the inverse trigonometric function
θ=arccos(6)
Calculate
θ∈/R
θ∈/Rcos(θ)=−6
Calculate
More Steps
Evaluate
cos(θ)=−6
Use the inverse trigonometric function
θ=arccos(−6)
Calculate
θ∈/R
θ∈/Rθ∈/R
Solution
θ∈/R
Alternative Form
No real solution
Show Solution
Graph
