Pergunta :
fractan^{2alpha + 1}sec{alpha} = secalpha
Resolva a equação
α=2π+kπ,k∈Z
Formulário Alternativo
α=90∘+180∘k,k∈Z
Calcule
sec(α)tan2(α)+1=sec(α)
Encontre o domínio
Mais Passos

Calcule
{α=2π+kπ,k∈Zsec(α)=0
Calcular
{α=2π+kπ,k∈Zα∈R
Encontre o cruzamento
α=2π+kπ,k∈Z
sec(α)tan2(α)+1=sec(α),α=2π+kπ,k∈Z
Use tan2(x)=sec2(x)−1 para reescrever a expressa˜o
sec(α)=sec(α)
Cancelar termos iguais em ambos os lados da expressão
0=0
A afirmac¸a˜o eˊ verdadeira para qualquer valor de α
α∈R
Verifique se a solução está no intervalo definido
α∈R,α=2π+kπ,k∈Z
Solução
α=2π+kπ,k∈Z
Formulário Alternativo
α=90∘+180∘k,k∈Z
Mostrar solução

Verifique a identidade
verdadeiro
Calcule
sec(α)tan2(α)+1=sec(α)
Comece a trabalhar no lado esquerdo
Mais Passos

Calcule
sec(α)tan2(α)+1
Use tant=costsint para transformar a expressa˜o
sec(α)(cos(α)sin(α))2+1
Reescrever a expressão
Mais Passos

Calcule
(cos(α)sin(α))2+1
Reescrever a expressão
cos2(α)sin2(α)+1
Reduza as frações a um denominador comum
cos2(α)sin2(α)+cos2(α)cos2(α)
Escreva todos os numeradores acima do denominador comum
cos2(α)sin2(α)+cos2(α)
sec(α)cos2(α)sin2(α)+cos2(α)
Multiplique pelo recíproco
cos2(α)sin2(α)+cos2(α)×sec(α)1
Multiplique os termos
cos2(α)sec(α)sin2(α)+cos2(α)
Transforme a expressão
Mais Passos

Calcule
cos2(α)sec(α)
Use sect=cost1 para transformar a expressa˜o
cos2(α)×cos(α)1
Cancele o fator comum cos(α)
cos(α)×1
Multiplique os termos
cos(α)
cos(α)sin2(α)+cos2(α)
Use sin2(t)+cos2(t)=1 para transformar a expressa˜o
cos(α)1
cos(α)1=sec(α)
Comece a trabalhar no lado direito
cos(α)1=cos(α)1
Solução
verdadeiro
Mostrar solução

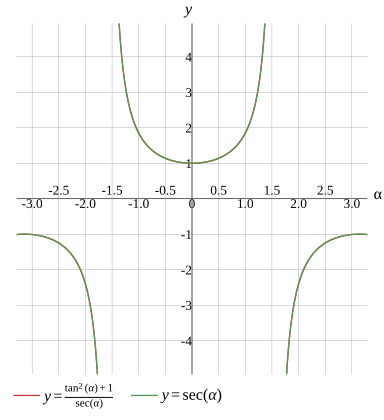
Gráfico