Question
Solve the equation
x1≈−4.215184,x2≈0.813694,x3≈3.401489
Evaluate
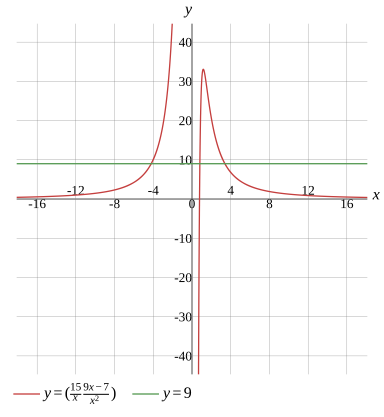
x15×x29x−7=9
Find the domain
More Steps


Evaluate
{x=0x2=0
The only way a power can not be 0 is when the base not equals 0
{x=0x=0
Find the intersection
x=0
x15×x29x−7=9,x=0
Multiply the terms
More Steps


Multiply the terms
x15×x29x−7
Multiply the terms
x×x215(9x−7)
Multiply the terms
More Steps


Evaluate
x×x2
Use the product rule an×am=an+m to simplify the expression
x1+2
Add the numbers
x3
x315(9x−7)
x315(9x−7)=9
Cross multiply
15(9x−7)=x3×9
Simplify the equation
15(9x−7)=9x3
Rewrite the expression
3×5(9x−7)=3×3x3
Evaluate
5(9x−7)=3x3
Expand the expression
More Steps


Evaluate
5(9x−7)
Apply the distributive property
5×9x−5×7
Multiply the numbers
45x−5×7
Multiply the numbers
45x−35
45x−35=3x3
Move the expression to the left side
45x−35−3x3=0
Calculate
x≈−4.215184x≈0.813694x≈3.401489
Check if the solution is in the defined range
x≈−4.215184x≈0.813694x≈3.401489,x=0
Find the intersection of the solution and the defined range
x≈−4.215184x≈0.813694x≈3.401489
Solution
x1≈−4.215184,x2≈0.813694,x3≈3.401489
Show Solution

Graph