Question
(x×1)x×(x−1)3=1
Solve the equation
x=4
Evaluate
(x×1)x×(x−1)3=1
Find the domain
More Steps


Evaluate
{x×1=0x−1=0
Any expression multiplied by 1 remains the same
{x=0x−1=0
Calculate
More Steps


Evaluate
x−1=0
Move the constant to the right side
x=0+1
Removing 0 doesn't change the value,so remove it from the expression
x=1
{x=0x=1
Find the intersection
x∈(−∞,0)∪(0,1)∪(1,+∞)
(x×1)x×(x−1)3=1,x∈(−∞,0)∪(0,1)∪(1,+∞)
Remove the parentheses
x×1x×x−13=1
Simplify
More Steps


Evaluate
x×1x×x−13
Reduce the fraction
More Steps


Evaluate
x×1x
Any expression multiplied by 1 remains the same
xx
Reduce the fraction
1
1×x−13
Calculate
x−13
x−13=1
Cross multiply
3=x−1
Swap the sides of the equation
x−1=3
Move the constant to the right side
x=3+1
Add the numbers
x=4
Check if the solution is in the defined range
x=4,x∈(−∞,0)∪(0,1)∪(1,+∞)
Solution
x=4
Show Solution

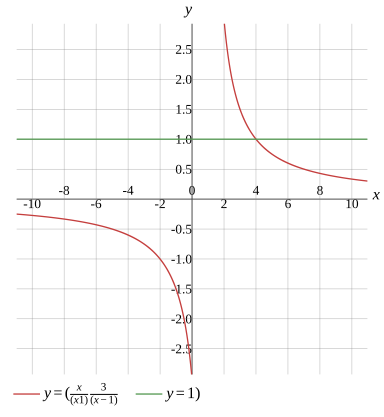
Graph