Question
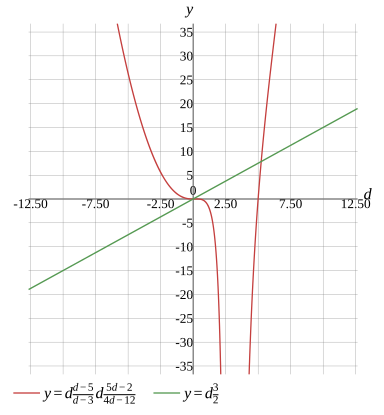
d×d−3d−5×d×4d−125d−2=d×23
Solve the equation
d1=0,d2≈5.237066
Evaluate
d×d−3d−5×d×4d−125d−2=d×23
Find the domain
More Steps


Evaluate
{d−3=04d−12=0
Calculate
More Steps


Evaluate
d−3=0
Move the constant to the right side
d=0+3
Removing 0 doesn't change the value,so remove it from the expression
d=3
{d=34d−12=0
Calculate
More Steps


Evaluate
4d−12=0
Move the constant to the right side
4d=0+12
Removing 0 doesn't change the value,so remove it from the expression
4d=12
Divide both sides
44d=412
Divide the numbers
d=412
Divide the numbers
d=3
{d=3d=3
Find the intersection
d=3
d×d−3d−5×d×4d−125d−2=d×23,d=3
Multiply
More Steps


Evaluate
d×d−3d−5×d×4d−125d−2
Multiply the terms
d2×d−3d−5×4d−125d−2
Multiply the terms
d−3d2(d−5)×4d−125d−2
Multiply the terms
(d−3)(4d−12)d2(d−5)(5d−2)
(d−3)(4d−12)d2(d−5)(5d−2)=d×23
Use the commutative property to reorder the terms
(d−3)(4d−12)d2(d−5)(5d−2)=23d
Rewrite the expression
(d−3)(4d−12)d2(d−5)(5d−2)=23d
Cross multiply
d2(d−5)(5d−2)×2=(d−3)(4d−12)×3d
Simplify the equation
2d2(d−5)(5d−2)=(d−3)(4d−12)×3d
Simplify the equation
2d2(d−5)(5d−2)=3(d−3)(4d−12)d
Rewrite the expression
2d2(d−5)(5d−2)=2×3(d−3)(2d−6)d
Evaluate
d2(d−5)(5d−2)=3(d−3)(2d−6)d
Calculate
More Steps


Calculate
d2(d−5)(5d−2)
Simplify
More Steps


Evaluate
d2(d−5)
Apply the distributive property
d2×d−d2×5
Multiply the terms
d3−d2×5
Use the commutative property to reorder the terms
d3−5d2
(d3−5d2)(5d−2)
Apply the distributive property
d3×5d−d3×2−5d2×5d−(−5d2×2)
Multiply the terms
More Steps


Evaluate
d3×5d
Use the commutative property to reorder the terms
5d3×d
Multiply the terms
5d4
5d4−d3×2−5d2×5d−(−5d2×2)
Use the commutative property to reorder the terms
5d4−2d3−5d2×5d−(−5d2×2)
Multiply the terms
More Steps


Evaluate
−5d2×5d
Multiply the numbers
−25d2×d
Multiply the terms
−25d3
5d4−2d3−25d3−(−5d2×2)
Multiply the numbers
5d4−2d3−25d3−(−10d2)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
5d4−2d3−25d3+10d2
Subtract the terms
More Steps


Evaluate
−2d3−25d3
Collect like terms by calculating the sum or difference of their coefficients
(−2−25)d3
Subtract the numbers
−27d3
5d4−27d3+10d2
5d4−27d3+10d2=3(d−3)(2d−6)d
Calculate
More Steps


Calculate
3(d−3)(2d−6)d
Simplify
More Steps


Evaluate
3(d−3)
Apply the distributive property
3d−3×3
Multiply the numbers
3d−9
(3d−9)(2d−6)d
Simplify
More Steps


Evaluate
(3d−9)(2d−6)
Apply the distributive property
3d×2d−3d×6−9×2d−(−9×6)
Multiply the terms
6d2−3d×6−9×2d−(−9×6)
Multiply the numbers
6d2−18d−9×2d−(−9×6)
Multiply the numbers
6d2−18d−18d−(−9×6)
Multiply the numbers
6d2−18d−18d−(−54)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
6d2−18d−18d+54
Subtract the terms
6d2−36d+54
(6d2−36d+54)d
Apply the distributive property
6d2×d−36d×d+54d
Multiply the terms
More Steps


Evaluate
d2×d
Use the product rule an×am=an+m to simplify the expression
d2+1
Add the numbers
d3
6d3−36d×d+54d
Multiply the terms
6d3−36d2+54d
5d4−27d3+10d2=6d3−36d2+54d
Move the expression to the left side
5d4−27d3+10d2−(6d3−36d2+54d)=0
Calculate the sum or difference
More Steps


Add the terms
5d4−27d3+10d2−(6d3−36d2+54d)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
5d4−27d3+10d2−6d3+36d2−54d
Subtract the terms
More Steps


Evaluate
−27d3−6d3
Collect like terms by calculating the sum or difference of their coefficients
(−27−6)d3
Subtract the numbers
−33d3
5d4−33d3+10d2+36d2−54d
Add the terms
More Steps


Evaluate
10d2+36d2
Collect like terms by calculating the sum or difference of their coefficients
(10+36)d2
Add the numbers
46d2
5d4−33d3+46d2−54d
5d4−33d3+46d2−54d=0
Factor the expression
d(5d3−33d2+46d−54)=0
Separate the equation into 2 possible cases
d=05d3−33d2+46d−54=0
Solve the equation
d=0d≈5.237066
Check if the solution is in the defined range
d=0d≈5.237066,d=3
Find the intersection of the solution and the defined range
d=0d≈5.237066
Solution
d1=0,d2≈5.237066
Show Solution

Graph