Solve \log_{7}\left(5x\right) 4\log_{7}\left(2\right)

Evaluate

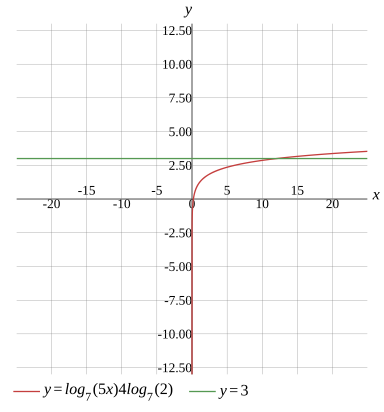
lo g_{7} (5 x) \times 4 lo g_{7} (2) = 3

Find the domain

More Steps

lo g_{7} (5 x) \times 4 lo g_{7} (2) = 3, x > 0

Multiply the terms

More Steps

4 lo g_{7} (2) \times lo g_{7} (5 x) = 3

Divide both sides

\frac{4 lo g _{7} ( 2 ) \times lo g _{7} ( 5 x )}{4 lo g _{7} ( 2 )} = \frac{3}{4 lo g _{7} ( 2 )}

Divide the numbers

lo g_{7} (5 x) = \frac{3}{4 lo g _{7} ( 2 )}

Evaluate the logarithm

lo g_{7} (5 x) = \frac{3}{lo g _{7} ( 2 ^{4} )}

Evaluate the logarithm

lo g_{7} (5 x) = 3 lo g_{2^{4}} (7)

Convert the logarithm into exponential form using the fact that lo g_{a} x = b is equal to x = a^{b}

5 x = 7^{3 l o g_{2^{4}} (7)}

Simplify

5 x = 7^{3 l o g_{16} (7)}

Divide both sides

\frac{5 x}{5} = \frac{7 ^{3 l o g_{16} (7)}}{5}

Divide the numbers

x = \frac{7 ^{3 l o g_{16} (7)}}{5}

Simplify

More Steps

x = \frac{4 7 ^{3 l o g_{2} (7)}}{5}

Check if the solution is in the defined range

x = \frac{4 7 ^{3 l o g_{2} (7)}}{5}, x > 0

Solution

x = \frac{4 7 ^{3 l o g_{2} (7)}}{5}

Alternative Form

x \approx 12.033656

Solve the equation