Solve \theta = 210 ^{\circ} - ScanMath

HOME CALCULATOR SOLVER

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... \theta = 210 ^{\circ}

Question

Solve the equation

θ = \frac{7 π}{6}

Alternative Form

θ \approx 3.665191

Show Solution

Rewrite the equation

3 y = 3 \times x

Show Solution

Find the coterminal angle

θ^{'} = - 15 0^{\circ}

Show Solution

Find the reference angle

θ^{'} = 6 0^{\circ}

Show Solution

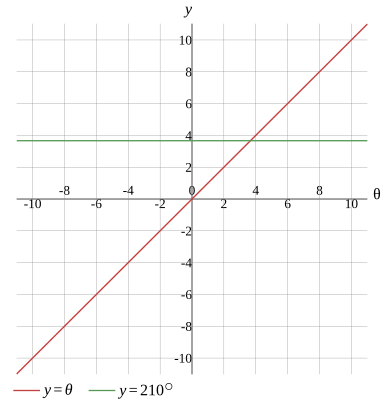
Graph

Graph