Solve |(3x-1)^2-5x^2-(2x-3)^2 7| 6=3|6x-1| - ScanMath

HOME CALCULATOR

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... |(3x-1)^2-5x^2-(2x-3)^2 7| 6=3|6x-1|

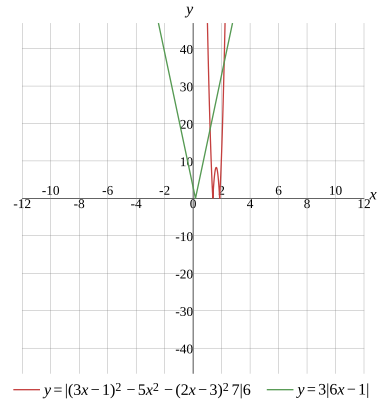
Question

Solve the equation

x_{1} = \frac{81 - 561}{48}, x_{2} = \frac{81 + 561}{48}

Alternative Form

x_{1} \approx 1.194053, x_{2} \approx 2.180947

Evaluate

(3 x - 1)^{2} - 5 x^{2} - (2 x - 3)^{2} \times 7 \times 6 = 3 ∣ 6 x - 1 ∣

Simplify

More Steps

6 24 x^{2} - 78 x + 62 = 3 ∣ 6 x - 1 ∣

Move the expression to the left side

6 24 x^{2} - 78 x + 62 - 3 ∣ 6 x - 1 ∣ = 0

Separate the equation into 4 possible cases

6 (24 x^{2} - 78 x + 62) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 \geq 0 6 (24 x^{2} - 78 x + 62) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the equation

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 \geq 0 6 (24 x^{2} - 78 x + 62) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), 6 x - 1 \geq 0 6 (24 x^{2} - 78 x + 62) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} 6 (24 x^{2} - 78 x + 62) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the equation

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, 24 x^{2} - 78 x + 62 \geq 0, 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), 6 x - 1 < 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} 6 (- (24 x^{2} - 78 x + 62)) - 3 (6 x - 1) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the equation

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, 6 x - 1 \geq 0 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} 6 (- (24 x^{2} - 78 x + 62)) - 3 (- (6 x - 1)) = 0, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the equation

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, 24 x^{2} - 78 x + 62 < 0, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, 6 x - 1 < 0

Solve the inequality

More Steps

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x \geq \frac{1}{6} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x < \frac{1}{6}

Find the intersection

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48} x \in / R, x \in (- \infty, \frac{- 33 + 39}{24}] \cup [\frac{33 + 39}{24}, + \infty), x < \frac{1}{6} x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x < \frac{1}{6}

Find the intersection

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48} x \in / R x \in / R, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x \geq \frac{1}{6} x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x < \frac{1}{6}

Find the intersection

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48} x \in / R x \in / R x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}, \frac{- 33 + 39}{24} < x < \frac{33 + 39}{24}, x < \frac{1}{6}

Find the intersection

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48} x \in / R x \in / R x \in \emptyset

Find the union

x = \frac{81 + 561}{48} x = \frac{81 - 561}{48}

Solution

x_{1} = \frac{81 - 561}{48}, x_{2} = \frac{81 + 561}{48}

Alternative Form

x_{1} \approx 1.194053, x_{2} \approx 2.180947

Show Solution

Graph

Graph