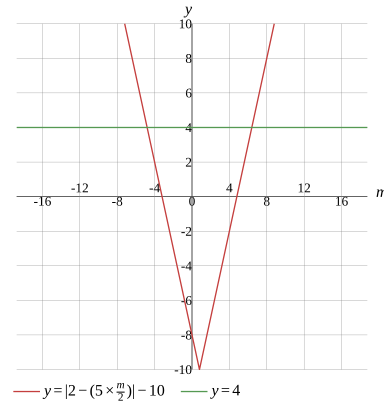
Question
Solve the equation
m1=−524,m2=532
Alternative Form
m1=−4.8,m2=6.4
Evaluate
2−(5×2m)−10=4
Multiply the terms
2−25m−10=4
Move the constant to the right-hand side and change its sign
2−25m=4+10
Add the numbers
2−25m=14
Separate the equation into 2 possible cases
2−25m=142−25m=−14
Solve the equation for m
More Steps


Evaluate
2−25m=14
Move the constant to the right-hand side and change its sign
−25m=14−2
Subtract the numbers
−25m=12
Rewrite the expression
2−5m=12
Cross multiply
−5m=2×12
Simplify the equation
−5m=24
Change the signs on both sides of the equation
5m=−24
Divide both sides
55m=5−24
Divide the numbers
m=5−24
Use b−a=−ba=−ba to rewrite the fraction
m=−524
m=−5242−25m=−14
Solve the equation for m
More Steps


Evaluate
2−25m=−14
Move the constant to the right-hand side and change its sign
−25m=−14−2
Subtract the numbers
−25m=−16
Rewrite the expression
2−5m=−16
Cross multiply
−5m=2(−16)
Simplify the equation
−5m=−32
Change the signs on both sides of the equation
5m=32
Divide both sides
55m=532
Divide the numbers
m=532
m=−524m=532
Solution
m1=−524,m2=532
Alternative Form
m1=−4.8,m2=6.4
Show Solution

Graph