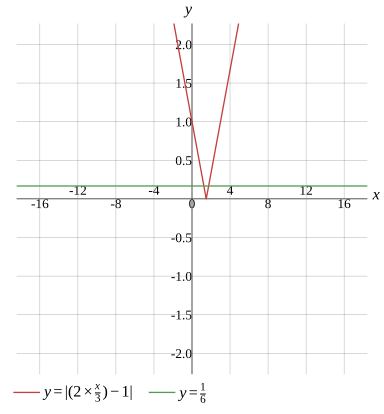
Question
Solve the equation
x1=45,x2=47
Alternative Form
x1=1.25,x2=1.75
Evaluate
(2×3x)−1=61
Multiply the terms
32x−1=61
Separate the equation into 2 possible cases
32x−1=6132x−1=−61
Solve the equation for x
More Steps


Evaluate
32x−1=61
Move the constant to the right-hand side and change its sign
32x=61+1
Add the numbers
More Steps


Evaluate
61+1
Reduce fractions to a common denominator
61+66
Write all numerators above the common denominator
61+6
Add the numbers
67
32x=67
Multiply both sides of the equation by 3
32x×3=67×3
Multiply the terms
2x=67×3
Divide the terms
2x=27
Multiply by the reciprocal
2x×21=27×21
Multiply
x=27×21
Multiply
More Steps


Evaluate
27×21
To multiply the fractions,multiply the numerators and denominators separately
2×27
Multiply the numbers
47
x=47
x=4732x−1=−61
Solve the equation for x
More Steps


Evaluate
32x−1=−61
Move the constant to the right-hand side and change its sign
32x=−61+1
Add the numbers
More Steps


Evaluate
−61+1
Reduce fractions to a common denominator
−61+66
Write all numerators above the common denominator
6−1+6
Add the numbers
65
32x=65
Multiply both sides of the equation by 3
32x×3=65×3
Multiply the terms
2x=65×3
Divide the terms
2x=25
Multiply by the reciprocal
2x×21=25×21
Multiply
x=25×21
Multiply
More Steps


Evaluate
25×21
To multiply the fractions,multiply the numerators and denominators separately
2×25
Multiply the numbers
45
x=45
x=47x=45
Solution
x1=45,x2=47
Alternative Form
x1=1.25,x2=1.75
Show Solution

Graph