Question
Solve the equation
x=1
Evaluate
∣2x×1∣−3∣1−x∣=2
Multiply the terms
∣2x∣−3∣1−x∣=2
Move the expression to the left side
∣2x∣−3∣1−x∣−2=0
Separate the equation into 4 possible cases
2x−3(1−x)−2=0,2x≥0,1−x≥02x−3(−(1−x))−2=0,2x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the equation
More Steps


Evaluate
2x−3(1−x)−2=0
Calculate
More Steps


Evaluate
2x−3(1−x)−2
Expand the expression
2x−3+3x−2
Add the terms
5x−3−2
Subtract the numbers
5x−5
5x−5=0
Move the constant to the right-hand side and change its sign
5x=0+5
Removing 0 doesn't change the value,so remove it from the expression
5x=5
Divide both sides
55x=55
Divide the numbers
x=55
Divide the numbers
More Steps


Evaluate
55
Reduce the numbers
11
Calculate
1
x=1
x=1,2x≥0,1−x≥02x−3(−(1−x))−2=0,2x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
x=1,x≥0,1−x≥02x−3(−(1−x))−2=0,2x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
More Steps


Evaluate
1−x≥0
Move the constant to the right side
−x≥0−1
Removing 0 doesn't change the value,so remove it from the expression
−x≥−1
Change the signs on both sides of the inequality and flip the inequality sign
x≤1
x=1,x≥0,x≤12x−3(−(1−x))−2=0,2x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the equation
More Steps


Evaluate
2x−3(−(1−x))−2=0
Calculate
2x−3(−1+x)−2=0
Calculate
More Steps


Evaluate
2x−3(−1+x)−2
Expand the expression
2x+3−3x−2
Subtract the terms
−x+3−2
Subtract the numbers
−x+1
−x+1=0
Move the constant to the right-hand side and change its sign
−x=0−1
Removing 0 doesn't change the value,so remove it from the expression
−x=−1
Change the signs on both sides of the equation
x=1
x=1,x≥0,x≤1x=1,2x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
x=1,x≥0,x≤1x=1,x≥0,1−x<0−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
More Steps


Evaluate
1−x<0
Move the constant to the right side
−x<0−1
Removing 0 doesn't change the value,so remove it from the expression
−x<−1
Change the signs on both sides of the inequality and flip the inequality sign
x>1
x=1,x≥0,x≤1x=1,x≥0,x>1−2x−3(1−x)−2=0,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the equation
More Steps


Evaluate
−2x−3(1−x)−2=0
Calculate
More Steps


Evaluate
−2x−3(1−x)−2
Expand the expression
−2x−3+3x−2
Add the terms
x−3−2
Subtract the numbers
x−5
x−5=0
Move the constant to the right-hand side and change its sign
x=0+5
Removing 0 doesn't change the value,so remove it from the expression
x=5
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,2x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,x<0,1−x≥0−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the inequality
More Steps


Evaluate
1−x≥0
Move the constant to the right side
−x≥0−1
Removing 0 doesn't change the value,so remove it from the expression
−x≥−1
Change the signs on both sides of the inequality and flip the inequality sign
x≤1
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,x<0,x≤1−2x−3(−(1−x))−2=0,2x<0,1−x<0
Solve the equation
More Steps


Evaluate
−2x−3(−(1−x))−2=0
Calculate
−2x−3(−1+x)−2=0
Calculate
More Steps


Evaluate
−2x−3(−1+x)−2
Expand the expression
−2x+3−3x−2
Subtract the terms
−5x+3−2
Subtract the numbers
−5x+1
−5x+1=0
Move the constant to the right-hand side and change its sign
−5x=0−1
Removing 0 doesn't change the value,so remove it from the expression
−5x=−1
Change the signs on both sides of the equation
5x=1
Divide both sides
55x=51
Divide the numbers
x=51
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,x<0,x≤1x=51,2x<0,1−x<0
Solve the inequality
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,x<0,x≤1x=51,x<0,1−x<0
Solve the inequality
More Steps


Evaluate
1−x<0
Move the constant to the right side
−x<0−1
Removing 0 doesn't change the value,so remove it from the expression
−x<−1
Change the signs on both sides of the inequality and flip the inequality sign
x>1
x=1,x≥0,x≤1x=1,x≥0,x>1x=5,x<0,x≤1x=51,x<0,x>1
Find the intersection
x=1x=1,x≥0,x>1x=5,x<0,x≤1x=51,x<0,x>1
Find the intersection
x=1x∈∅x=5,x<0,x≤1x=51,x<0,x>1
Find the intersection
x=1x∈∅x∈∅x=51,x<0,x>1
Find the intersection
x=1x∈∅x∈∅x∈∅
Solution
x=1
Show Solution

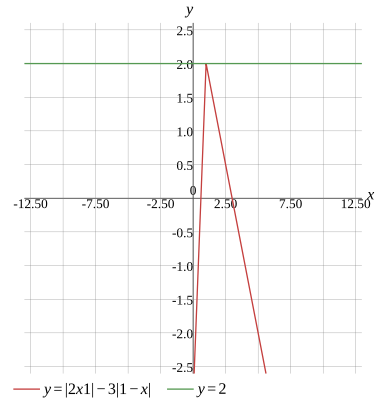
Graph