Algebra
Calculus
Trigonometry
Matrix
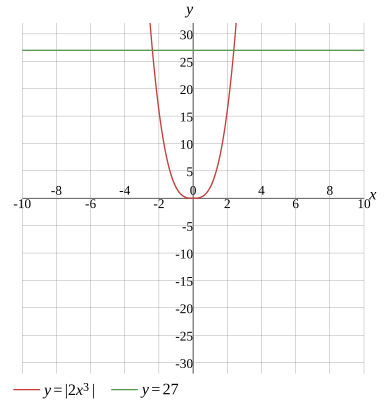
Question
Solve the equation
x1=−2334,x2=2334
Alternative Form
x1≈−2.381102,x2≈2.381102
Evaluate
2x3=27
Separate the equation into 2 possible cases
2x3=272x3=−27
Solve the equation for x
More Steps
Evaluate
2x3=27
Divide both sides
22x3=227
Divide the numbers
x3=227
Take the 3-th root on both sides of the equation
3x3=3227
Calculate
x=3227
Simplify the root
More Steps
Evaluate
3227
To take a root of a fraction,take the root of the numerator and denominator separately
32327
Simplify the radical expression
323
Multiply by the Conjugate
32×3223322
Simplify
32×322334
Multiply the numbers
2334
x=2334
x=23342x3=−27
Solve the equation for x
More Steps
Evaluate
2x3=−27
Divide both sides
22x3=2−27
Divide the numbers
x3=2−27
Use b−a=−ba=−ba to rewrite the fraction
x3=−227
Take the 3-th root on both sides of the equation
3x3=3−227
Calculate
x=3−227
Simplify the root
More Steps
Evaluate
3−227
An odd root of a negative radicand is always a negative
−3227
To take a root of a fraction,take the root of the numerator and denominator separately
−32327
Simplify the radical expression
−323
Multiply by the Conjugate
32×322−3322
Simplify
32×322−334
Multiply the numbers
2−334
Calculate
−2334
x=−2334
x=2334x=−2334
Solution
x1=−2334,x2=2334
Alternative Form
x1≈−2.381102,x2≈2.381102
Show Solution
Graph
