Solve |5x^3| 3 = 8

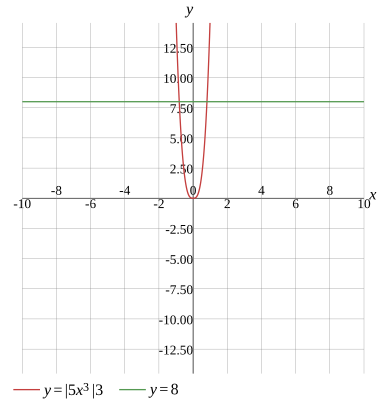
Question

Solve the equation

x_{1} = - \frac{2 3 225}{15}, x_{2} = \frac{2 3 225}{15}

Alternative Form

x_{1} \approx - 0.81096, x_{2} \approx 0.81096

Evaluate

5 x^{3} \times 3 = 8

Multiply the terms

3 5 x^{3} = 8

Divide both sides

\frac{3 5 x ^{3}}{3} = \frac{8}{3}

Divide the numbers

5 x^{3} = \frac{8}{3}

Separate the equation into 2 possible cases

5 x^{3} = \frac{8}{3} 5 x^{3} = - \frac{8}{3}

Solve the equation for x

More Steps

x = \frac{2 3 225}{15} 5 x^{3} = - \frac{8}{3}

Solve the equation for x

More Steps

x = \frac{2 3 225}{15} x = - \frac{2 3 225}{15}

Solution

x_{1} = - \frac{2 3 225}{15}, x_{2} = \frac{2 3 225}{15}

Alternative Form

x_{1} \approx - 0.81096, x_{2} \approx 0.81096

Show Solution