Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
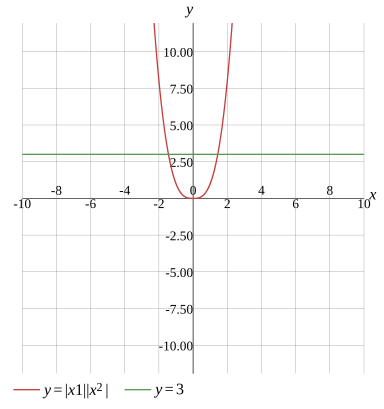
x1=−33,x2=33
Alternative Form
x1≈−1.44225,x2≈1.44225
Evaluate
∣x×1∣x2=3
Simplify
More Steps
Evaluate
∣x×1∣x2
Any expression multiplied by 1 remains the same
∣x∣x2
When the expression in absolute value bars is not negative, remove the bars
∣x∣×x2
Calculate
x2∣x∣
x2∣x∣=3
Separate the equation into 2 possible cases
x2×x=3,x≥0x2(−x)=3,x<0
Evaluate
More Steps
Evaluate
x2×x=3
Expand the expression
More Steps
Evaluate
x2×x
Use the product rule an×am=an+m to simplify the expression
x2+1
Add the numbers
x3
x3=3
Take the 3-th root on both sides of the equation
3x3=33
Calculate
x=33
x=33,x≥0x2(−x)=3,x<0
Evaluate
More Steps
Evaluate
x2(−x)=3
Calculate
−x2×x=3
Expand the expression
More Steps
Evaluate
x2×x
Use the product rule an×am=an+m to simplify the expression
x2+1
Add the numbers
x3
−x3=3
Change the signs on both sides of the equation
x3=−3
Take the 3-th root on both sides of the equation
3x3=3−3
Calculate
x=3−3
An odd root of a negative radicand is always a negative
x=−33
x=33,x≥0x=−33,x<0
Find the intersection
x=33x=−33,x<0
Find the intersection
x=33x=−33
Solution
x1=−33,x2=33
Alternative Form
x1≈−1.44225,x2≈1.44225
Show Solution
Graph
