Solve |x^2*1|-|x^2-x 1|=|2x 1|

Evaluate

x^{2} \times 1 - x^{2} - x \times 1 = ∣ 2 x \times 1 ∣

Simplify

More Steps

x^{2} - x^{2} - x = ∣ 2 x \times 1 ∣

Multiply the terms

x^{2} - x^{2} - x = ∣ 2 x ∣

Swap the sides

∣ 2 x ∣ = x^{2} - x^{2} - x

Move the expression to the left side

∣ 2 x ∣ - (x^{2} - x^{2} - x) = 0

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

∣ 2 x ∣ - x^{2} + x^{2} - x = 0

Separate the equation into 4 possible cases

2 x - x^{2} + x^{2} - x = 0, 2 x \geq 0, x^{2} - x \geq 0 2 x - x^{2} - (x^{2} - x) = 0, 2 x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Calculate the sum or difference

More Steps

x = 0, 2 x \geq 0, x^{2} - x \geq 0 2 x - x^{2} - (x^{2} - x) = 0, 2 x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

x = 0, x \geq 0, x^{2} - x \geq 0 2 x - x^{2} - (x^{2} - x) = 0, 2 x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) 2 x - x^{2} - (x^{2} - x) = 0, 2 x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the equation

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, 2 x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, x^{2} - x < 0 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 - 2 x - x^{2} + x^{2} - x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the equation

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, 2 x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x^{2} - x \geq 0 - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the inequality

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) - 2 x - x^{2} - (x^{2} - x) = 0, 2 x < 0, x^{2} - x < 0

Solve the equation

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = - \frac{1}{2}, 2 x < 0, x^{2} - x < 0

Solve the inequality

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = - \frac{1}{2}, x < 0, x^{2} - x < 0

Solve the inequality

More Steps

x = 0, x \geq 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = - \frac{1}{2}, x < 0, 0 < x < 1

Find the intersection

x = 0 x = 0 x = \frac{3}{2}, x \geq 0, 0 < x < 1 x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = - \frac{1}{2}, x < 0, 0 < x < 1

Find the intersection

x = 0 x \in \emptyset x = 0, x < 0, x \in (- \infty, 0] \cup [1, + \infty) x = 0 x = - \frac{1}{2}, x < 0, 0 < x < 1

Find the intersection

x = 0 x \in \emptyset x \in \emptyset x = 0 x = - \frac{1}{2}, x < 0, 0 < x < 1

Find the intersection

x = 0 x \in \emptyset x \in \emptyset x \in \emptyset

Solution

x = 0

Solve the equation

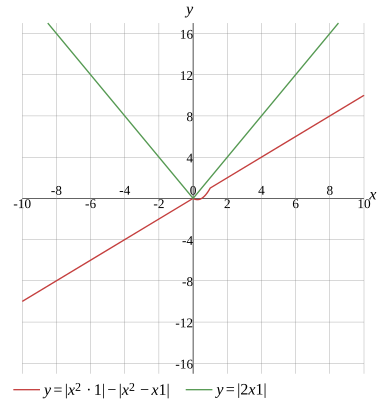
Graph