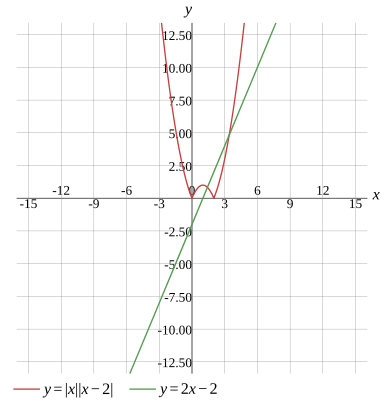
Question
Solve the equation
x1=2,x2=2+2
Alternative Form
x1≈1.414214,x2≈3.414214
Evaluate
∣x∣∣x−2∣=2x−2
Multiply the terms
∣x(x−2)∣=2x−2
Rewrite the expression
∣x(x−2)∣−2x+2=0
Separate the equation into 2 possible cases
x(x−2)−2x+2=0,x(x−2)≥0−x(x−2)−2x+2=0,x(x−2)<0
Solve the equation
More Steps


Evaluate
x(x−2)−2x+2=0
Calculate the sum or difference
More Steps


Evaluate
x(x−2)−2x+2
Expand the expression
x2−2x−2x+2
Subtract the terms
x2−4x+2
x2−4x+2=0
Substitute a=1,b=−4 and c=2 into the quadratic formula x=2a−b±b2−4ac
x=24±(−4)2−4×2
Simplify the expression
More Steps


Evaluate
(−4)2−4×2
Multiply the numbers
(−4)2−8
Rewrite the expression
42−8
Evaluate the power
16−8
Subtract the numbers
8
x=24±8
Simplify the radical expression
More Steps


Evaluate
8
Write the expression as a product where the root of one of the factors can be evaluated
4×2
Write the number in exponential form with the base of 2
22×2
The root of a product is equal to the product of the roots of each factor
22×2
Reduce the index of the radical and exponent with 2
22
x=24±22
Separate the equation into 2 possible cases
x=24+22x=24−22
Simplify the expression
x=2+2x=24−22
Simplify the expression
x=2+2x=2−2
x=2+2x=2−2,x(x−2)≥0−x(x−2)−2x+2=0,x(x−2)<0
Solve the inequality
More Steps


Evaluate
x(x−2)≥0
Separate the inequality into 2 possible cases
{x≥0x−2≥0{x≤0x−2≤0
Solve the inequality
More Steps


Evaluate
x−2≥0
Move the constant to the right side
x≥0+2
Removing 0 doesn't change the value,so remove it from the expression
x≥2
{x≥0x≥2{x≤0x−2≤0
Solve the inequality
More Steps


Evaluate
x−2≤0
Move the constant to the right side
x≤0+2
Removing 0 doesn't change the value,so remove it from the expression
x≤2
{x≥0x≥2{x≤0x≤2
Find the intersection
x≥2{x≤0x≤2
Find the intersection
x≥2x≤0
Find the union
x∈(−∞,0]∪[2,+∞)
x=2+2x=2−2,x∈(−∞,0]∪[2,+∞)−x(x−2)−2x+2=0,x(x−2)<0
Solve the equation
More Steps


Evaluate
−x(x−2)−2x+2=0
Calculate
More Steps


Evaluate
−x(x−2)−2x
Expand the expression
−x2+2x−2x
The sum of two opposites equals 0
−x2+0
Remove 0
−x2
−x2+2=0
Move the constant to the right-hand side and change its sign
−x2=0−2
Removing 0 doesn't change the value,so remove it from the expression
−x2=−2
Change the signs on both sides of the equation
x2=2
Take the root of both sides of the equation and remember to use both positive and negative roots
x=±2
Separate the equation into 2 possible cases
x=2x=−2
x=2+2x=2−2,x∈(−∞,0]∪[2,+∞)x=2x=−2,x(x−2)<0
Solve the inequality
More Steps


Evaluate
x(x−2)<0
Separate the inequality into 2 possible cases
{x>0x−2<0{x<0x−2>0
Solve the inequality
More Steps


Evaluate
x−2<0
Move the constant to the right side
x<0+2
Removing 0 doesn't change the value,so remove it from the expression
x<2
{x>0x<2{x<0x−2>0
Solve the inequality
More Steps


Evaluate
x−2>0
Move the constant to the right side
x>0+2
Removing 0 doesn't change the value,so remove it from the expression
x>2
{x>0x<2{x<0x>2
Find the intersection
0<x<2{x<0x>2
Find the intersection
0<x<2x∈∅
Find the union
0<x<2
x=2+2x=2−2,x∈(−∞,0]∪[2,+∞)x=2x=−2,0<x<2
Find the intersection
x=2+2x=2x=−2,0<x<2
Find the intersection
x=2+2x=2
Solution
x1=2,x2=2+2
Alternative Form
x1≈1.414214,x2≈3.414214
Show Solution

Graph