Solve |x-|4-x|| -2x = 4

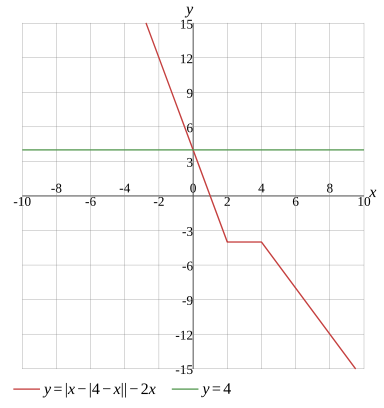
Question

Solve the equation

x = 0

Evaluate

∣ x - ∣ 4 - x ∣ ∣ - 2 x = 4

Move the expression to the left side

∣ x - ∣ 4 - x ∣ ∣ - 2 x - 4 = 0

Separate the equation into 2 possible cases

x - ∣ 4 - x ∣ - 2 x - 4 = 0, x - ∣ 4 - x ∣ \geq 0 - (x - ∣ 4 - x ∣) - 2 x - 4 = 0, x - ∣ 4 - x ∣ < 0

Solve the equation

More Steps

Evaluate

x - ∣ 4 - x ∣ - 2 x - 4 = 0

Calculate

More Steps

Evaluate

x - 2 x

Collect like terms by calculating the sum or difference of their coefficients

(1 - 2) x

Subtract the numbers

- x

- x - ∣ 4 - x ∣ - 4 = 0

Separate the equation into 2 possible cases

- x - (4 - x) - 4 = 0, 4 - x \geq 0 - x - (- (4 - x)) - 4 = 0, 4 - x < 0

The statement is false for any value of x

More Steps

Evaluate

- x - (4 - x) - 4 = 0

Calculate

- x - 4 + x - 4 = 0

Calculate the sum or difference

- 8 = 0

The statement is false for any value of x

x \in \emptyset

x \in \emptyset, 4 - x \geq 0 - x - (- (4 - x)) - 4 = 0, 4 - x < 0

Solve the inequality

More Steps

Evaluate

4 - x \geq 0

Move the constant to the right side

- x \geq 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x \geq - 4

Change the signs on both sides of the inequality and flip the inequality sign

x \leq 4

x \in \emptyset, x \leq 4 - x - (- (4 - x)) - 4 = 0, 4 - x < 0

Solve the equation

More Steps

Evaluate

- x - (- (4 - x)) - 4 = 0

Calculate

- x + 4 - x - 4 = 0

Calculate the sum or difference

- 2 x = 0

Change the signs on both sides of the equation

2 x = 0

Rewrite the expression

x = 0

x \in \emptyset, x \leq 4 x = 0, 4 - x < 0

Solve the inequality

More Steps

Evaluate

4 - x < 0

Move the constant to the right side

- x < 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x < - 4

Change the signs on both sides of the inequality and flip the inequality sign

x > 4

x \in \emptyset, x \leq 4 x = 0, x > 4

Find the intersection

x \in \emptyset x = 0, x > 4

Find the intersection

x \in \emptyset x \in \emptyset

Find the union

x \in \emptyset

x \in \emptyset, x - ∣ 4 - x ∣ \geq 0 - (x - ∣ 4 - x ∣) - 2 x - 4 = 0, x - ∣ 4 - x ∣ < 0

Solve the inequality

More Steps

Evaluate

x - ∣ 4 - x ∣ \geq 0

Separate the inequality into 2 possible cases

x - (4 - x) \geq 0, 4 - x \geq 0 x - (- (4 - x)) \geq 0, 4 - x < 0

Evaluate

More Steps

Evaluate

x - (4 - x) \geq 0

Remove the parentheses

x - 4 + x \geq 0

Simplify the expression

2 x - 4 \geq 0

Move the constant to the right side

2 x \geq 0 + 4

Removing 0 doesn't change the value,so remove it from the expression

2 x \geq 4

Divide both sides

\frac{2 x}{2} \geq \frac{4}{2}

Divide the numbers

x \geq \frac{4}{2}

Divide the numbers

x \geq 2

x \geq 2, 4 - x \geq 0 x - (- (4 - x)) \geq 0, 4 - x < 0

Evaluate

More Steps

Evaluate

4 - x \geq 0

Move the constant to the right side

- x \geq 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x \geq - 4

Change the signs on both sides of the inequality and flip the inequality sign

x \leq 4

x \geq 2, x \leq 4 x - (- (4 - x)) \geq 0, 4 - x < 0

The statement is true for any value of x

More Steps

Evaluate

x - (- (4 - x)) \geq 0

Remove the parentheses

x + 4 - x \geq 0

Simplify the expression

4 \geq 0

The statement is true for any value of x

x \in R

x \geq 2, x \leq 4 x \in R, 4 - x < 0

Evaluate

More Steps

Evaluate

4 - x < 0

Move the constant to the right side

- x < 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x < - 4

Change the signs on both sides of the inequality and flip the inequality sign

x > 4

x \geq 2, x \leq 4 x \in R, x > 4

Find the intersection

2 \leq x \leq 4 x \in R, x > 4

Find the intersection

2 \leq x \leq 4 x > 4

Find the union

x \geq 2

x \in \emptyset, x \geq 2 - (x - ∣ 4 - x ∣) - 2 x - 4 = 0, x - ∣ 4 - x ∣ < 0

Solve the equation

More Steps

Evaluate

- (x - ∣ 4 - x ∣) - 2 x - 4 = 0

Calculate

- x + ∣ 4 - x ∣ - 2 x - 4 = 0

Calculate

More Steps

Evaluate

- x - 2 x

Collect like terms by calculating the sum or difference of their coefficients

(- 1 - 2) x

Subtract the numbers

- 3 x

- 3 x + ∣ 4 - x ∣ - 4 = 0

Separate the equation into 2 possible cases

- 3 x + 4 - x - 4 = 0, 4 - x \geq 0 - 3 x - (4 - x) - 4 = 0, 4 - x < 0

Solve the equation

More Steps

Evaluate

- 3 x + 4 - x - 4 = 0

Calculate the sum or difference

- 4 x = 0

Change the signs on both sides of the equation

4 x = 0

Rewrite the expression

x = 0

x = 0, 4 - x \geq 0 - 3 x - (4 - x) - 4 = 0, 4 - x < 0

Solve the inequality

More Steps

Evaluate

4 - x \geq 0

Move the constant to the right side

- x \geq 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x \geq - 4

Change the signs on both sides of the inequality and flip the inequality sign

x \leq 4

x = 0, x \leq 4 - 3 x - (4 - x) - 4 = 0, 4 - x < 0

Solve the equation

More Steps

Evaluate

- 3 x - (4 - x) - 4 = 0

Calculate

- 3 x - 4 + x - 4 = 0

Calculate the sum or difference

- 2 x - 8 = 0

Move the constant to the right-hand side and change its sign

- 2 x = 0 + 8

Removing 0 doesn't change the value,so remove it from the expression

- 2 x = 8

Change the signs on both sides of the equation

2 x = - 8

Divide both sides

\frac{2 x}{2} = \frac{- 8}{2}

Divide the numbers

x = \frac{- 8}{2}

Divide the numbers

x = - 4

x = 0, x \leq 4 x = - 4, 4 - x < 0

Solve the inequality

More Steps

Evaluate

4 - x < 0

Move the constant to the right side

- x < 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x < - 4

Change the signs on both sides of the inequality and flip the inequality sign

x > 4

x = 0, x \leq 4 x = - 4, x > 4

Find the intersection

x = 0 x = - 4, x > 4

Find the intersection

x = 0 x \in \emptyset

Find the union

x = 0

x \in \emptyset, x \geq 2 x = 0, x - ∣ 4 - x ∣ < 0

Solve the inequality

More Steps

Evaluate

x - ∣ 4 - x ∣ < 0

Separate the inequality into 2 possible cases

x - (4 - x) < 0, 4 - x \geq 0 x - (- (4 - x)) < 0, 4 - x < 0

Evaluate

More Steps

Evaluate

x - (4 - x) < 0

Remove the parentheses

x - 4 + x < 0

Simplify the expression

2 x - 4 < 0

Move the constant to the right side

2 x < 0 + 4

Removing 0 doesn't change the value,so remove it from the expression

2 x < 4

Divide both sides

\frac{2 x}{2} < \frac{4}{2}

Divide the numbers

x < \frac{4}{2}

Divide the numbers

x < 2

x < 2, 4 - x \geq 0 x - (- (4 - x)) < 0, 4 - x < 0

Evaluate

More Steps

Evaluate

4 - x \geq 0

Move the constant to the right side

- x \geq 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x \geq - 4

Change the signs on both sides of the inequality and flip the inequality sign

x \leq 4

x < 2, x \leq 4 x - (- (4 - x)) < 0, 4 - x < 0

The statement is false for any value of x

More Steps

Evaluate

x - (- (4 - x)) < 0

Remove the parentheses

x + 4 - x < 0

Simplify the expression

4 < 0

The statement is false for any value of x

x \in \emptyset

x < 2, x \leq 4 x \in \emptyset, 4 - x < 0

Evaluate

More Steps

Evaluate

4 - x < 0

Move the constant to the right side

- x < 0 - 4

Removing 0 doesn't change the value,so remove it from the expression

- x < - 4

Change the signs on both sides of the inequality and flip the inequality sign

x > 4

x < 2, x \leq 4 x \in \emptyset, x > 4

Find the intersection

x < 2 x \in \emptyset, x > 4

Find the intersection

x < 2 x \in \emptyset

Find the union

x < 2

x \in \emptyset, x \geq 2 x = 0, x < 2

Find the intersection

x \in \emptyset x = 0, x < 2

Find the intersection

x \in \emptyset x = 0

Solution

x = 0

Show Solution

Solve the equation

Graph