Question
Solve the equation
x=21
Alternative Form
x=0.5
Evaluate
(2x−1)×3=25(2x−1)
Multiply the terms
3(2x−1)=25(2x−1)
Calculate
More Steps


Evaluate
3(2x−1)
Apply the distributive property
3×2x−3×1
Multiply the numbers
6x−3×1
Any expression multiplied by 1 remains the same
6x−3
6x−3=25(2x−1)
Calculate
More Steps


Evaluate
25(2x−1)
Apply the distributive property
25×2x−25×1
Multiply the numbers
50x−25×1
Any expression multiplied by 1 remains the same
50x−25
6x−3=50x−25
Move the expression to the left side
6x−3−(50x−25)=0
Calculate
More Steps


Add the terms
6x−3−(50x−25)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
6x−3−50x+25
Subtract the terms
More Steps


Evaluate
6x−50x
Collect like terms by calculating the sum or difference of their coefficients
(6−50)x
Subtract the numbers
−44x
−44x−3+25
Add the numbers
−44x+22
−44x+22=0
Move the constant to the right-hand side and change its sign
−44x=0−22
Removing 0 doesn't change the value,so remove it from the expression
−44x=−22
Change the signs on both sides of the equation
44x=22
Divide both sides
4444x=4422
Divide the numbers
x=4422
Solution
x=21
Alternative Form
x=0.5
Show Solution

Rewrite the equation
2x=1
Evaluate
(2x−1)×3=25(2x−1)
Evaluate
3(2x−1)=25(2x−1)
Multiply
More Steps


Evaluate
3(2x−1)
Apply the distributive property
3×2x−3×1
Multiply the numbers
6x−3×1
Any expression multiplied by 1 remains the same
6x−3
6x−3=25(2x−1)
Multiply
More Steps


Evaluate
25(2x−1)
Apply the distributive property
25×2x−25×1
Multiply the numbers
50x−25×1
Any expression multiplied by 1 remains the same
50x−25
6x−3=50x−25
Move the variable to the left side
−44x−3=−25
Move the constant to the right side
−44x=−22
Multiply both sides
44x=22
Solution
2x=1
Show Solution

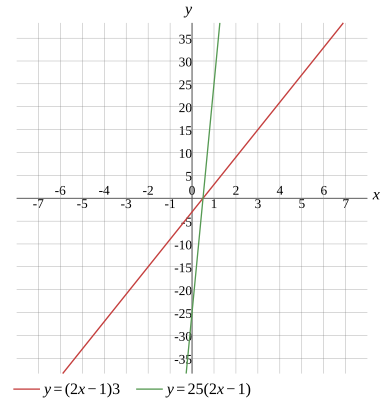
Graph