Question
Solve the equation(The real numbers system)
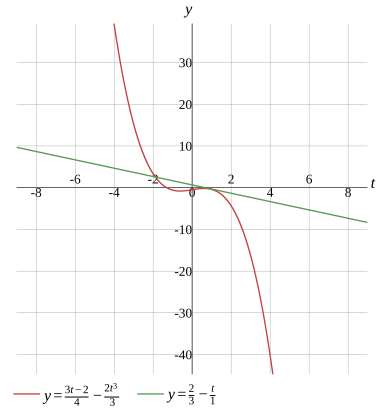
t≈−1.885037
Evaluate
43t−2−32t3=32−1t
Evaluate
43t−2−32t3=32−t
Multiply both sides of the equation by LCD
(43t−2−32t3)×12=(32−t)×12
Simplify the equation
More Steps


Evaluate
(43t−2−32t3)×12
Apply the distributive property
43t−2×12−32t3×12
Simplify
(3t−2)×3−2t3×4
Multiply the terms
More Steps


Evaluate
(3t−2)×3
Apply the distributive property
3t×3−2×3
Calculate
9t−2×3
Calculate
9t−6
9t−6−2t3×4
Multiply the numbers
9t−6−8t3
9t−6−8t3=(32−t)×12
Simplify the equation
More Steps


Evaluate
(32−t)×12
Apply the distributive property
32×12−t×12
Simplify
2×4−t×12
Multiply the numbers
8−t×12
Use the commutative property to reorder the terms
8−12t
9t−6−8t3=8−12t
Move the expression to the left side
9t−6−8t3−(8−12t)=0
Subtract the terms
More Steps


Evaluate
9t−6−8t3−(8−12t)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
9t−6−8t3−8+12t
Add the terms
More Steps


Evaluate
9t+12t
Collect like terms by calculating the sum or difference of their coefficients
(9+12)t
Add the numbers
21t
21t−6−8t3−8
Subtract the numbers
21t−14−8t3
21t−14−8t3=0
Solution
t≈−1.885037
Show Solution

Solve the equation(The complex numbers system)
t1≈0.942518−0.200057i,t2≈0.942518+0.200057i,t3≈−1.885037
Evaluate
43t−2−32t3=32−1t
Divide the terms
43t−2−32t3=32−t
Multiply both sides of the equation by LCD
(43t−2−32t3)×12=(32−t)×12
Simplify the equation
More Steps


Evaluate
(43t−2−32t3)×12
Apply the distributive property
43t−2×12−32t3×12
Simplify
(3t−2)×3−2t3×4
Multiply the terms
More Steps


Evaluate
(3t−2)×3
Apply the distributive property
3t×3−2×3
Calculate
9t−2×3
Calculate
9t−6
9t−6−2t3×4
Multiply the numbers
9t−6−8t3
9t−6−8t3=(32−t)×12
Simplify the equation
More Steps


Evaluate
(32−t)×12
Apply the distributive property
32×12−t×12
Simplify
2×4−t×12
Multiply the numbers
8−t×12
Use the commutative property to reorder the terms
8−12t
9t−6−8t3=8−12t
Move the expression to the left side
9t−6−8t3−(8−12t)=0
Subtract the terms
More Steps


Evaluate
9t−6−8t3−(8−12t)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
9t−6−8t3−8+12t
Add the terms
More Steps


Evaluate
9t+12t
Collect like terms by calculating the sum or difference of their coefficients
(9+12)t
Add the numbers
21t
21t−6−8t3−8
Subtract the numbers
21t−14−8t3
21t−14−8t3=0
Calculate
t≈−1.885037t≈0.942518+0.200057it≈0.942518−0.200057i
Solution
t1≈0.942518−0.200057i,t2≈0.942518+0.200057i,t3≈−1.885037
Show Solution

Graph