Question
Solve the equation
x≈1.342298
Evaluate
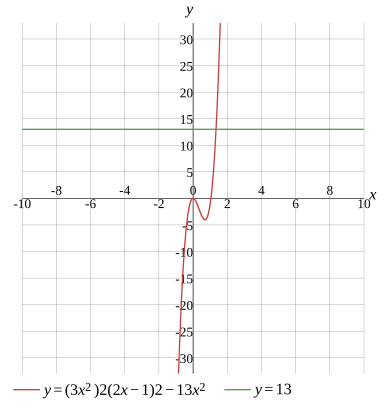
3x2×2(2x−1)×2−13x2=13
Multiply the terms
More Steps


Evaluate
3×2×2
Multiply the terms
6×2
Multiply the numbers
12
12x2(2x−1)−13x2=13
Move the expression to the left side
12x2(2x−1)−13x2−13=0
Calculate
More Steps


Evaluate
12x2(2x−1)−13x2−13
Expand the expression
More Steps


Calculate
12x2(2x−1)
Apply the distributive property
12x2×2x−12x2×1
Multiply the terms
24x3−12x2×1
Any expression multiplied by 1 remains the same
24x3−12x2
24x3−12x2−13x2−13
Subtract the terms
More Steps


Evaluate
−12x2−13x2
Collect like terms by calculating the sum or difference of their coefficients
(−12−13)x2
Subtract the numbers
−25x2
24x3−25x2−13
24x3−25x2−13=0
Solution
x≈1.342298
Show Solution

Graph