Question
Solve the equation
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
Alternative Form
x≈{17.141173∘+360∘k162.858827∘+360∘k,k∈Z
Alternative Form
x≈{0.29917+2kπ2.842423+2kπ,k∈Z
Evaluate
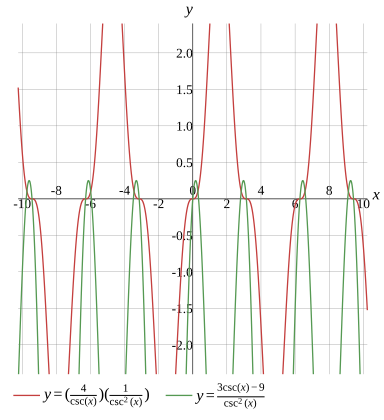
(csc(x)4)(csc2(x)1)=csc2(x)3csc(x)−9
Find the domain
More Steps


Evaluate
⎩⎨⎧x=kπ,k∈Zcsc(x)=0csc2(x)=0
Calculate
⎩⎨⎧x=kπ,k∈Zx∈Rcsc2(x)=0
Calculate
⎩⎨⎧x=kπ,k∈Zx∈Rx∈R
Simplify
{x=kπ,k∈Zx∈R
Find the intersection
x=kπ,k∈Z
(csc(x)4)(csc2(x)1)=csc2(x)3csc(x)−9,x=kπ,k∈Z
Simplify
More Steps


Evaluate
(csc(x)4)(csc2(x)1)
Remove the unnecessary parentheses
csc(x)4×(csc2(x)1)
Remove the unnecessary parentheses
csc(x)4×csc2(x)1
Multiply the terms
csc(x)csc2(x)4
Multiply the terms
csc3(x)4
csc3(x)4=csc2(x)3csc(x)−9
Cross multiply
4csc2(x)=csc3(x)(3csc(x)−9)
Move the expression to the left side
4csc2(x)−csc3(x)(3csc(x)−9)=0
Factor the expression
More Steps


Calculate
4csc2(x)−csc3(x)(3csc(x)−9)
Rewrite the expression
4csc2(x)−3csc4(x)+9csc3(x)
Rewrite the expression
csc2(x)×4−csc2(x)×3csc2(x)+csc2(x)×9csc(x)
Factor out csc2(x) from the expression
csc2(x)(4−3csc2(x)+9csc(x))
csc2(x)(4−3csc2(x)+9csc(x))=0
Separate the equation into 2 possible cases
csc2(x)=04−3csc2(x)+9csc(x)=0
Solve the equation
More Steps


Evaluate
csc2(x)=0
The only way a power can be 0 is when the base equals 0
csc(x)=0
Use the inverse trigonometric function
x=arccsc(0)
Calculate
x∈/R
x∈/R4−3csc2(x)+9csc(x)=0
Solve the equation
More Steps


Evaluate
4−3csc2(x)+9csc(x)=0
Rewrite in standard form
−3csc2(x)+9csc(x)+4=0
Multiply both sides
3csc2(x)−9csc(x)−4=0
Substitute a=3,b=−9 and c=−4 into the quadratic formula csc(x)=2a−b±b2−4ac
csc(x)=2×39±(−9)2−4×3(−4)
Simplify the expression
csc(x)=69±(−9)2−4×3(−4)
Simplify the expression
More Steps


Evaluate
(−9)2−4×3(−4)
Multiply
(−9)2−(−48)
Rewrite the expression
92−(−48)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
92+48
Evaluate the power
81+48
Add the numbers
129
csc(x)=69±129
Separate the equation into 2 possible cases
csc(x)=69+129csc(x)=69−129
Rearrange the terms
csc(x)=69+129x∈/R
Calculate
More Steps


Evaluate
csc(x)=69+129
Use the inverse trigonometric function
x=arccsc(69+129)
Calculate
x=arccsc(69+129)x=−arccsc(69+129)+π
Add the period of 2kπ,k∈Z to find all solutions
x=arccsc(69+129)+2kπ,k∈Zx=−arccsc(69+129)+π+2kπ,k∈Z
Find the union
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Zx∈/R
Find the union
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
x∈/Rx=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
Find the union
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
Check if the solution is in the defined range
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z,x=kπ,k∈Z
Solution
x=⎩⎨⎧arccsc(69+129)+2kπ−arccsc(69+129)+π+2kπ,k∈Z
Alternative Form
x≈{17.141173∘+360∘k162.858827∘+360∘k,k∈Z
Alternative Form
x≈{0.29917+2kπ2.842423+2kπ,k∈Z
Show Solution

Graph