Question
Solve the equation(The real numbers system)
x∈/R
Alternative Form
No real solution
Evaluate
25x−3=−(x−2)2×4
Use the commutative property to reorder the terms
25x−3=−4(x−2)2
Swap the sides
−4(x−2)2=25x−3
Expand the expression
More Steps


Evaluate
−4(x−2)2
Expand the expression
More Steps


Evaluate
(x−2)2
Use (a−b)2=a2−2ab+b2 to expand the expression
x2−2x×2+22
Calculate
x2−4x+4
−4(x2−4x+4)
Apply the distributive property
−4x2−(−4×4x)−4×4
Multiply the numbers
−4x2−(−16x)−4×4
Multiply the numbers
−4x2−(−16x)−16
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−4x2+16x−16
−4x2+16x−16=25x−3
Move the expression to the left side
−4x2+227x−13=0
Multiply both sides
4x2−227x+13=0
Multiply both sides
2(4x2−227x+13)=2×0
Calculate
8x2−27x+26=0
Substitute a=8,b=−27 and c=26 into the quadratic formula x=2a−b±b2−4ac
x=2×827±(−27)2−4×8×26
Simplify the expression
x=1627±(−27)2−4×8×26
Simplify the expression
More Steps


Evaluate
(−27)2−4×8×26
Multiply the terms
More Steps


Multiply the terms
4×8×26
Multiply the terms
32×26
Multiply the numbers
832
(−27)2−832
Rewrite the expression
272−832
Evaluate the power
729−832
Subtract the numbers
−103
x=1627±−103
Solution
x∈/R
Alternative Form
No real solution
Show Solution

Solve the equation(The complex numbers system)
Solve using the quadratic formula in the complex numbers system
Solve by completing the square in the complex numbers system
Solve using the PQ formula in the complex numbers system
x1=1627−16103i,x2=1627+16103i
Alternative Form
x1≈1.6875−0.634306i,x2≈1.6875+0.634306i
Evaluate
25x−3=−(x−2)2×4
Use the commutative property to reorder the terms
25x−3=−4(x−2)2
Swap the sides
−4(x−2)2=25x−3
Expand the expression
More Steps


Evaluate
−4(x−2)2
Expand the expression
More Steps


Evaluate
(x−2)2
Use (a−b)2=a2−2ab+b2 to expand the expression
x2−2x×2+22
Calculate
x2−4x+4
−4(x2−4x+4)
Apply the distributive property
−4x2−(−4×4x)−4×4
Multiply the numbers
−4x2−(−16x)−4×4
Multiply the numbers
−4x2−(−16x)−16
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−4x2+16x−16
−4x2+16x−16=25x−3
Move the expression to the left side
−4x2+227x−13=0
Multiply both sides
4x2−227x+13=0
Multiply both sides
2(4x2−227x+13)=2×0
Calculate
8x2−27x+26=0
Substitute a=8,b=−27 and c=26 into the quadratic formula x=2a−b±b2−4ac
x=2×827±(−27)2−4×8×26
Simplify the expression
x=1627±(−27)2−4×8×26
Simplify the expression
More Steps


Evaluate
(−27)2−4×8×26
Multiply the terms
More Steps


Multiply the terms
4×8×26
Multiply the terms
32×26
Multiply the numbers
832
(−27)2−832
Rewrite the expression
272−832
Evaluate the power
729−832
Subtract the numbers
−103
x=1627±−103
Simplify the radical expression
More Steps


Evaluate
−103
Evaluate the power
103×−1
Evaluate the power
103×i
x=1627±103×i
Separate the equation into 2 possible cases
x=1627+103×ix=1627−103×i
Simplify the expression
x=1627+16103ix=1627−103×i
Simplify the expression
x=1627+16103ix=1627−16103i
Solution
x1=1627−16103i,x2=1627+16103i
Alternative Form
x1≈1.6875−0.634306i,x2≈1.6875+0.634306i
Show Solution

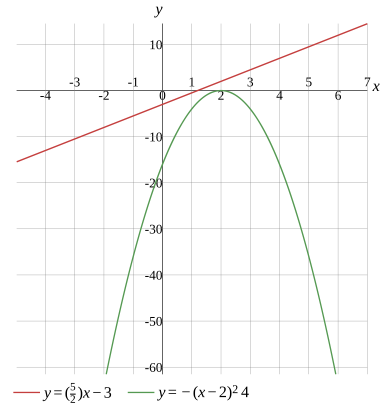
Graph