Question
Solve the equation(The real numbers system)
x∈/R
Alternative Form
No real solution
Evaluate
2x−1×3x−2=4x−3
Multiply the terms
More Steps


Multiply the terms
2x−1×3x−2
Multiply the terms
2×3(x−1)(x−2)
Multiply the terms
6(x−1)(x−2)
6(x−1)(x−2)=4x−3
Rewrite the expression
61x2−21x+31=4x−3
Rewrite the expression
61x2−21x+31=41x−43
Move the expression to the left side
61x2−43x+1213=0
Multiply both sides
12(61x2−43x+1213)=12×0
Calculate
2x2−9x+13=0
Substitute a=2,b=−9 and c=13 into the quadratic formula x=2a−b±b2−4ac
x=2×29±(−9)2−4×2×13
Simplify the expression
x=49±(−9)2−4×2×13
Simplify the expression
More Steps


Evaluate
(−9)2−4×2×13
Multiply the terms
More Steps


Multiply the terms
4×2×13
Multiply the terms
8×13
Multiply the numbers
104
(−9)2−104
Rewrite the expression
92−104
Evaluate the power
81−104
Subtract the numbers
−23
x=49±−23
Solution
x∈/R
Alternative Form
No real solution
Show Solution

Solve the equation(The complex numbers system)
Solve using the quadratic formula in the complex numbers system
Solve using the PQ formula in the complex numbers system
x1=49−423i,x2=49+423i
Alternative Form
x1≈2.25−1.198958i,x2≈2.25+1.198958i
Evaluate
2x−1×3x−2=4x−3
Multiply the terms
More Steps


Multiply the terms
2x−1×3x−2
Multiply the terms
2×3(x−1)(x−2)
Multiply the terms
6(x−1)(x−2)
6(x−1)(x−2)=4x−3
Rewrite the expression
61x2−21x+31=4x−3
Rewrite the expression
61x2−21x+31=41x−43
Move the expression to the left side
61x2−43x+1213=0
Multiply both sides
12(61x2−43x+1213)=12×0
Calculate
2x2−9x+13=0
Substitute a=2,b=−9 and c=13 into the quadratic formula x=2a−b±b2−4ac
x=2×29±(−9)2−4×2×13
Simplify the expression
x=49±(−9)2−4×2×13
Simplify the expression
More Steps


Evaluate
(−9)2−4×2×13
Multiply the terms
More Steps


Multiply the terms
4×2×13
Multiply the terms
8×13
Multiply the numbers
104
(−9)2−104
Rewrite the expression
92−104
Evaluate the power
81−104
Subtract the numbers
−23
x=49±−23
Simplify the radical expression
More Steps


Evaluate
−23
Evaluate the power
23×−1
Evaluate the power
23×i
x=49±23×i
Separate the equation into 2 possible cases
x=49+23×ix=49−23×i
Simplify the expression
x=49+423ix=49−23×i
Simplify the expression
x=49+423ix=49−423i
Solution
x1=49−423i,x2=49+423i
Alternative Form
x1≈2.25−1.198958i,x2≈2.25+1.198958i
Show Solution

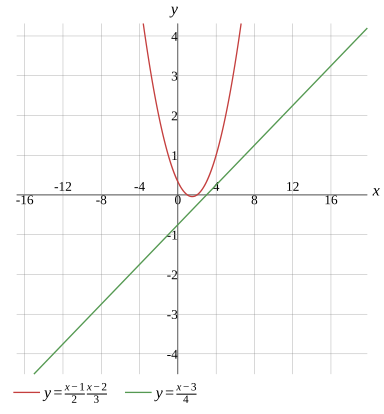
Graph