Algebra
Calculus
Trigonometry
Matrix
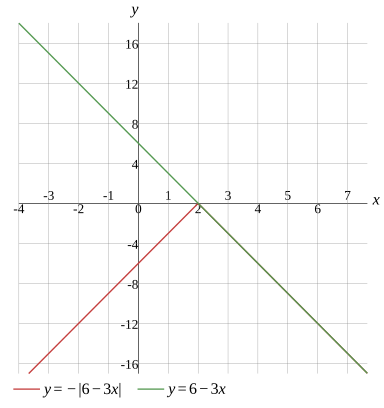
Question
Solve the equation
x≥2
Alternative Form
x∈[2,+∞)
Evaluate
−∣6−3x∣=6−3x
Rewrite the expression
−∣6−3x∣−6+3x=0
Separate the equation into 2 possible cases
−(6−3x)−6+3x=0,6−3x≥0−(−(6−3x))−6+3x=0,6−3x<0
Solve the equation
More Steps
Evaluate
−(6−3x)−6+3x=0
Calculate
−6+3x−6+3x=0
Calculate the sum or difference
More Steps
Evaluate
−6+3x−6+3x
Subtract the numbers
−12+3x+3x
Add the terms
−12+6x
−12+6x=0
Move the constant to the right-hand side and change its sign
6x=0+12
Removing 0 doesn't change the value,so remove it from the expression
6x=12
Divide both sides
66x=612
Divide the numbers
x=612
Divide the numbers
More Steps
Evaluate
612
Reduce the numbers
12
Calculate
2
x=2
x=2,6−3x≥0−(−(6−3x))−6+3x=0,6−3x<0
Solve the inequality
More Steps
Evaluate
6−3x≥0
Move the constant to the right side
−3x≥0−6
Removing 0 doesn't change the value,so remove it from the expression
−3x≥−6
Change the signs on both sides of the inequality and flip the inequality sign
3x≤6
Divide both sides
33x≤36
Divide the numbers
x≤36
Divide the numbers
More Steps
Evaluate
36
Reduce the numbers
12
Calculate
2
x≤2
x=2,x≤2−(−(6−3x))−6+3x=0,6−3x<0
The statement is true for any value of x
More Steps
Evaluate
−(−(6−3x))−6+3x=0
Calculate
6−3x−6+3x=0
Calculate the sum or difference
More Steps
Evaluate
6−3x−6+3x
Since two opposites add up to 0,remove them form the expression
−3x+3x
Add the terms
0
0=0
The statement is true for any value of x
x∈R
x=2,x≤2x∈R,6−3x<0
Solve the inequality
More Steps
Evaluate
6−3x<0
Move the constant to the right side
−3x<0−6
Removing 0 doesn't change the value,so remove it from the expression
−3x<−6
Change the signs on both sides of the inequality and flip the inequality sign
3x>6
Divide both sides
33x>36
Divide the numbers
x>36
Divide the numbers
More Steps
Evaluate
36
Reduce the numbers
12
Calculate
2
x>2
x=2,x≤2x∈R,x>2
Find the intersection
x=2x∈R,x>2
Find the intersection
x=2x>2
Solution
x≥2
Alternative Form
x∈[2,+∞)
Show Solution
Graph
