Question
Solve the equation
r=−225
Alternative Form
r=−12.5
Evaluate
−53r=721
Covert the mixed number to an improper fraction
More Steps


Evaluate
721
Multiply the denominator of the fraction by the whole number and add the numerator of the fraction
27×2+1
Multiply the terms
214+1
Add the terms
215
−53r=215
Change the signs on both sides of the equation
53r=−215
Multiply by the reciprocal
53r×35=−215×35
Multiply
r=−215×35
Solution
More Steps


Evaluate
−215×35
Reduce the numbers
−25×5
Multiply the numbers
−25×5
Multiply the numbers
−225
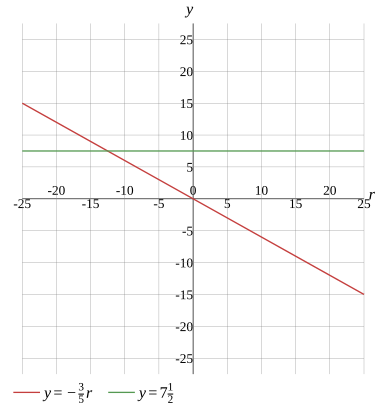
r=−225
Alternative Form
r=−12.5
Show Solution

Rewrite the equation
4x2+4y2=625
Evaluate
−53r=721
Evaluate
More Steps


Evaluate
721
Multiply the denominator of the fraction by the whole number and add the numerator of the fraction
27×2+1
Multiply the terms
214+1
Add the terms
215
−53r=215
Multiply both sides of the equation by LCD
−53r×10=215×10
Simplify the equation
More Steps


Evaluate
−53r×10
Simplify
−3r×2
Multiply the numbers
−6r
−6r=215×10
Simplify the equation
More Steps


Evaluate
215×10
Simplify
15×5
Multiply the numbers
75
−6r=75
Divide both sides of the equation by −3
2r=−25
Square both sides of the equation
(2r)2=(−25)2
Evaluate
4r2=(−25)2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
4(x2+y2)=(−25)2
Evaluate the power
4(x2+y2)=625
Solution
4x2+4y2=625
Show Solution

Graph