Algebra
Calculus
Trigonometry
Matrix
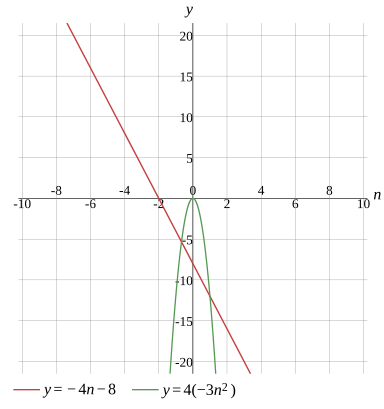
Question
Solve the quadratic equation
Solve by factoring
Solve using the quadratic formula
Solve by completing the square
Load more
n1=−32,n2=1
Alternative Form
n1=−0.6˙,n2=1
Evaluate
−4n−8=4(−3n2)
Multiply the numbers
More Steps
Evaluate
4(−3)
Multiplying or dividing an odd number of negative terms equals a negative
−4×3
Multiply the numbers
−12
−4n−8=−12n2
Swap the sides
−12n2=−4n−8
Move the expression to the left side
−12n2+4n+8=0
Factor the expression
More Steps
Evaluate
−12n2+4n+8
Rewrite the expression
−4×3n2+4n+4×2
Factor out −4 from the expression
−4(3n2−n−2)
Factor the expression
More Steps
Evaluate
3n2−n−2
Rewrite the expression
3n2+(2−3)n−2
Calculate
3n2+2n−3n−2
Rewrite the expression
n×3n+n×2−3n−2
Factor out n from the expression
n(3n+2)−3n−2
Factor out −1 from the expression
n(3n+2)−(3n+2)
Factor out 3n+2 from the expression
(n−1)(3n+2)
−4(n−1)(3n+2)
−4(n−1)(3n+2)=0
Divide the terms
(n−1)(3n+2)=0
When the product of factors equals 0,at least one factor is 0
n−1=03n+2=0
Solve the equation for n
More Steps
Evaluate
n−1=0
Move the constant to the right-hand side and change its sign
n=0+1
Removing 0 doesn't change the value,so remove it from the expression
n=1
n=13n+2=0
Solve the equation for n
More Steps
Evaluate
3n+2=0
Move the constant to the right-hand side and change its sign
3n=0−2
Removing 0 doesn't change the value,so remove it from the expression
3n=−2
Divide both sides
33n=3−2
Divide the numbers
n=3−2
Use b−a=−ba=−ba to rewrite the fraction
n=−32
n=1n=−32
Solution
n1=−32,n2=1
Alternative Form
n1=−0.6˙,n2=1
Show Solution
Graph
