Question
Solve the quadratic equation
Solve using the quadratic formula
Solve by completing the square
Solve using the PQ formula
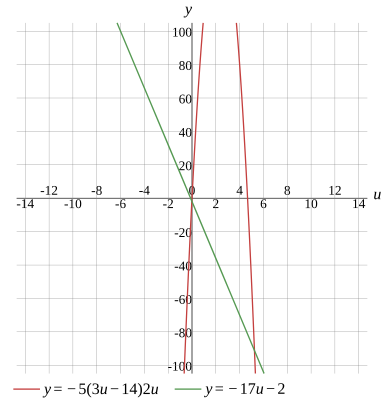
u1=60157−24889,u2=60157+24889
Alternative Form
u1≈−0.012708,u2≈5.246041
Evaluate
−5(3u−14)×2u=−17u−2
Multiply
More Steps


Evaluate
−5(3u−14)×2u
Multiply the terms
−10(3u−14)u
Multiply the terms
−10u(3u−14)
−10u(3u−14)=−17u−2
Expand the expression
More Steps


Evaluate
−10u(3u−14)
Apply the distributive property
−10u×3u−(−10u×14)
Multiply the terms
More Steps


Evaluate
−10u×3u
Multiply the numbers
−30u×u
Multiply the terms
−30u2
−30u2−(−10u×14)
Multiply the numbers
−30u2−(−140u)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−30u2+140u
−30u2+140u=−17u−2
Move the expression to the left side
−30u2+157u+2=0
Multiply both sides
30u2−157u−2=0
Substitute a=30,b=−157 and c=−2 into the quadratic formula u=2a−b±b2−4ac
u=2×30157±(−157)2−4×30(−2)
Simplify the expression
u=60157±(−157)2−4×30(−2)
Simplify the expression
More Steps


Evaluate
(−157)2−4×30(−2)
Multiply
More Steps


Multiply the terms
4×30(−2)
Rewrite the expression
−4×30×2
Multiply the terms
−240
(−157)2−(−240)
Rewrite the expression
1572−(−240)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
1572+240
Evaluate the power
24649+240
Add the numbers
24889
u=60157±24889
Separate the equation into 2 possible cases
u=60157+24889u=60157−24889
Solution
u1=60157−24889,u2=60157+24889
Alternative Form
u1≈−0.012708,u2≈5.246041
Show Solution

Graph