Solve -5x |3x-6|=1

Question

Solve the equation

x = \frac{15 - 4 15}{15}

Alternative Form

x \approx - 0.032796

Evaluate

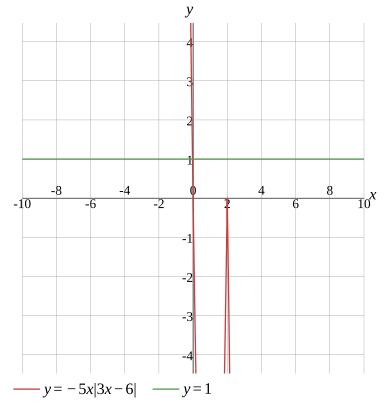
- 5 x ∣ 3 x - 6 ∣ = 1

Change the sign

5 x ∣ 3 x - 6 ∣ = - 1

Separate the equation into 2 possible cases

5 x (3 x - 6) = - 1, 3 x - 6 \geq 0 5 x (- (3 x - 6)) = - 1, 3 x - 6 < 0

Evaluate

More Steps

Evaluate

5 x (3 x - 6) = - 1

Expand the expression

More Steps

Evaluate

5 x (3 x - 6)

Apply the distributive property

5 x \times 3 x - 5 x \times 6

Multiply the terms

15 x^{2} - 5 x \times 6

Multiply the numbers

15 x^{2} - 30 x

15 x^{2} - 30 x = - 1

Move the expression to the left side

15 x^{2} - 30 x - (- 1) = 0

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

15 x^{2} - 30 x + 1 = 0

Substitute a= 15,b= - 30 and c= 1 into the quadratic formula x = \frac{- b \pm b ^{2} - 4 a c}{2 a}

x = \frac{30 \pm ( - 30 ) ^{2} - 4 \times 15}{2 \times 15}

Simplify the expression

x = \frac{30 \pm ( - 30 ) ^{2} - 4 \times 15}{30}

Simplify the expression

More Steps

Evaluate

(- 30)^{2} - 4 \times 15

Multiply the numbers

(- 30)^{2} - 60

Rewrite the expression

3 0^{2} - 60

Evaluate the power

900 - 60

Subtract the numbers

840

x = \frac{30 \pm 840}{30}

Simplify the radical expression

More Steps

Evaluate

840

Write the expression as a product where the root of one of the factors can be evaluated

4 \times 210

Write the number in exponential form with the base of 2

2^{2} \times 210

The root of a product is equal to the product of the roots of each factor

2^{2} \times 210

Reduce the index of the radical and exponent with 2

2210

x = \frac{30 \pm 2 210}{30}

Separate the equation into 2 possible cases

x = \frac{30 + 2 210}{30} x = \frac{30 - 2 210}{30}

Simplify the expression

x = \frac{15 + 210}{15} x = \frac{30 - 2 210}{30}

Simplify the expression

x = \frac{15 + 210}{15} x = \frac{15 - 210}{15}

x = \frac{15 + 210}{15} x = \frac{15 - 210}{15}, 3 x - 6 \geq 0 5 x (- (3 x - 6)) = - 1, 3 x - 6 < 0

Evaluate

More Steps

Evaluate

3 x - 6 \geq 0

Move the constant to the right side

3 x \geq 0 + 6

Removing 0 doesn't change the value,so remove it from the expression

3 x \geq 6

Divide both sides

\frac{3 x}{3} \geq \frac{6}{3}

Divide the numbers

x \geq \frac{6}{3}

Divide the numbers

More Steps

Evaluate

\frac{6}{3}

Reduce the numbers

\frac{2}{1}

Calculate

2

x \geq 2

x = \frac{15 + 210}{15} x = \frac{15 - 210}{15}, x \geq 2 5 x (- (3 x - 6)) = - 1, 3 x - 6 < 0

Evaluate

More Steps

Evaluate

5 x (- (3 x - 6)) = - 1

Remove the parentheses

5 x (- 3 x + 6) = - 1

Expand the expression

More Steps

Evaluate

5 x (- 3 x + 6)

Apply the distributive property

5 x (- 3 x) + 5 x \times 6

Multiply the terms

- 15 x^{2} + 5 x \times 6

Multiply the numbers

- 15 x^{2} + 30 x

- 15 x^{2} + 30 x = - 1

Move the expression to the left side

- 15 x^{2} + 30 x - (- 1) = 0

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

- 15 x^{2} + 30 x + 1 = 0

Multiply both sides

15 x^{2} - 30 x - 1 = 0

Substitute a= 15,b= - 30 and c= - 1 into the quadratic formula x = \frac{- b \pm b ^{2} - 4 a c}{2 a}

x = \frac{30 \pm ( - 30 ) ^{2} - 4 \times 15 ( - 1 )}{2 \times 15}

Simplify the expression

x = \frac{30 \pm ( - 30 ) ^{2} - 4 \times 15 ( - 1 )}{30}

Simplify the expression

More Steps

Evaluate

(- 30)^{2} - 4 \times 15 (- 1)

Multiply

(- 30)^{2} - (- 60)

Rewrite the expression

3 0^{2} - (- 60)

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

3 0^{2} + 60

Evaluate the power

900 + 60

Add the numbers

960

x = \frac{30 \pm 960}{30}

Simplify the radical expression

More Steps

Evaluate

960

Write the expression as a product where the root of one of the factors can be evaluated

64 \times 15

Write the number in exponential form with the base of 8

8^{2} \times 15

The root of a product is equal to the product of the roots of each factor

8^{2} \times 15

Reduce the index of the radical and exponent with 2

815

x = \frac{30 \pm 8 15}{30}

Separate the equation into 2 possible cases

x = \frac{30 + 8 15}{30} x = \frac{30 - 8 15}{30}

Simplify the expression

x = \frac{15 + 4 15}{15} x = \frac{30 - 8 15}{30}

Simplify the expression

x = \frac{15 + 4 15}{15} x = \frac{15 - 4 15}{15}

x = \frac{15 + 210}{15} x = \frac{15 - 210}{15}, x \geq 2 x = \frac{15 + 4 15}{15} x = \frac{15 - 4 15}{15}, 3 x - 6 < 0

Evaluate

More Steps

Evaluate

3 x - 6 < 0

Move the constant to the right side

3 x < 0 + 6

Removing 0 doesn't change the value,so remove it from the expression

3 x < 6

Divide both sides

\frac{3 x}{3} < \frac{6}{3}

Divide the numbers

x < \frac{6}{3}

Divide the numbers

More Steps

Evaluate

\frac{6}{3}

Reduce the numbers

\frac{2}{1}

Calculate

2

x < 2

x = \frac{15 + 210}{15} x = \frac{15 - 210}{15}, x \geq 2 x = \frac{15 + 4 15}{15} x = \frac{15 - 4 15}{15}, x < 2

Find the intersection

x \in \emptyset x = \frac{15 + 4 15}{15} x = \frac{15 - 4 15}{15}, x < 2

Find the intersection

x \in \emptyset x = \frac{15 - 4 15}{15}

Solution

x = \frac{15 - 4 15}{15}

Alternative Form

x \approx - 0.032796

Show Solution

Solve the equation

Graph