Question
Solve the inequality
Solve for x
Solve for g
Solve for l
Load more

x∈(−∞,0)∪(2,3)
Evaluate
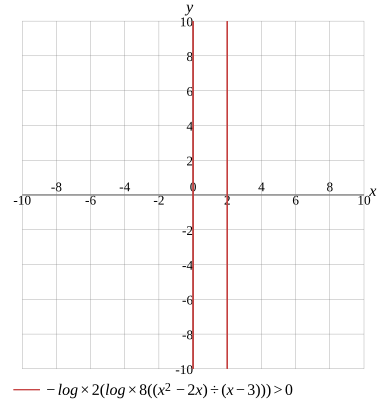
−log×2(log×8((x2−2x)÷(x−3)))>0
Remove the parentheses
−log×2log×8((x2−2x)÷(x−3))>0
Simplify
More Steps


Evaluate
−log×2log×8((x2−2x)÷(x−3))
Rewrite the expression
−log×2log×8×x−3x2−2x
Multiply
More Steps


Multiply the terms
log×2log×8×x−3x2−2x
Multiply the terms
l2og×2og×8×x−3x2−2x
Multiply the terms
l2o2g×2g×8×x−3x2−2x
Multiply the terms
l2o2g2×2×8×x−3x2−2x
Multiply the terms
l2o2g2×16×x−3x2−2x
Use the commutative property to reorder the terms
16l2o2g2×x−3x2−2x
Multiply the terms
x−316l2o2g2(x2−2x)
−x−316l2o2g2(x2−2x)
−x−316l2o2g2(x2−2x)>0
Change the signs on both sides of the inequality and flip the inequality sign
x−316l2o2g2(x2−2x)<0
Separate the inequality into 2 possible cases
{16l2o2g2(x2−2x)>0x−3<0{16l2o2g2(x2−2x)<0x−3>0
Solve the inequality
More Steps


Evaluate
16l2o2g2(x2−2x)>0
Rewrite the expression
x2−2x>0
Add the same value to both sides
x2−2x+1>1
Evaluate
(x−1)2>1
Take the 2-th root on both sides of the inequality
(x−1)2>1
Calculate
∣x−1∣>1
Separate the inequality into 2 possible cases
x−1>1x−1<−1
Calculate
More Steps


Evaluate
x−1>1
Move the constant to the right side
x>1+1
Add the numbers
x>2
x>2x−1<−1
Cancel equal terms on both sides of the expression
x>2x<0
Find the union
x∈(−∞,0)∪(2,+∞)
{x∈(−∞,0)∪(2,+∞)x−3<0{16l2o2g2(x2−2x)<0x−3>0
Solve the inequality
More Steps


Evaluate
x−3<0
Move the constant to the right side
x<0+3
Removing 0 doesn't change the value,so remove it from the expression
x<3
{x∈(−∞,0)∪(2,+∞)x<3{16l2o2g2(x2−2x)<0x−3>0
Solve the inequality
More Steps


Evaluate
16l2o2g2(x2−2x)<0
Rewrite the expression
x2−2x<0
Add the same value to both sides
x2−2x+1<1
Evaluate
(x−1)2<1
Take the 2-th root on both sides of the inequality
(x−1)2<1
Calculate
∣x−1∣<1
Separate the inequality into 2 possible cases
{x−1<1x−1>−1
Calculate
More Steps


Evaluate
x−1<1
Move the constant to the right side
x<1+1
Add the numbers
x<2
{x<2x−1>−1
Cancel equal terms on both sides of the expression
{x<2x>0
Find the intersection
0<x<2
{x∈(−∞,0)∪(2,+∞)x<3{0<x<2x−3>0
Solve the inequality
More Steps


Evaluate
x−3>0
Move the constant to the right side
x>0+3
Removing 0 doesn't change the value,so remove it from the expression
x>3
{x∈(−∞,0)∪(2,+∞)x<3{0<x<2x>3
Find the intersection
x∈(−∞,0)∪(2,3){0<x<2x>3
Find the intersection
x∈(−∞,0)∪(2,3)x∈∅
Find the union
x∈(−∞,0)∪(2,3)
Check if the solution is in the defined range
x∈(−∞,0)∪(2,3),x=3
Solution
x∈(−∞,0)∪(2,3)
Show Solution

Graph