Question
Solve the equation(The real numbers system)
r∈/R
Alternative Form
No real solution
Evaluate
710−71r=−72r2×75
Multiply the terms
More Steps


Evaluate
72×75
To multiply the fractions,multiply the numerators and denominators separately
7×72×5
Multiply the numbers
7×710
Multiply the numbers
4910
710−71r=−4910r2
Swap the sides
−4910r2=710−71r
Move the expression to the left side
−4910r2−710+71r=0
Rewrite in standard form
−4910r2+71r−710=0
Multiply both sides
4910r2−71r+710=0
Multiply both sides
49(4910r2−71r+710)=49×0
Calculate
10r2−7r+70=0
Substitute a=10,b=−7 and c=70 into the quadratic formula r=2a−b±b2−4ac
r=2×107±(−7)2−4×10×70
Simplify the expression
r=207±(−7)2−4×10×70
Simplify the expression
More Steps


Evaluate
(−7)2−4×10×70
Multiply the numbers
More Steps


Multiply the terms
4×10×70
Multiply the terms
40×70
Multiply the numbers
2800
(−7)2−2800
Rewrite the expression
72−2800
Evaluate the power
49−2800
Subtract the numbers
−2751
r=207±−2751
Solution
r∈/R
Alternative Form
No real solution
Show Solution

Solve the equation(The complex numbers system)
Solve using the quadratic formula in the complex numbers system
Solve by completing the square in the complex numbers system
Solve using the PQ formula in the complex numbers system
r1=207−202751i,r2=207+202751i
Alternative Form
r1≈0.35−2.622499i,r2≈0.35+2.622499i
Evaluate
710−71r=−72r2×75
Multiply the terms
More Steps


Evaluate
72×75
To multiply the fractions,multiply the numerators and denominators separately
7×72×5
Multiply the numbers
7×710
Multiply the numbers
4910
710−71r=−4910r2
Swap the sides
−4910r2=710−71r
Move the expression to the left side
−4910r2−710+71r=0
Rewrite in standard form
−4910r2+71r−710=0
Multiply both sides
4910r2−71r+710=0
Multiply both sides
49(4910r2−71r+710)=49×0
Calculate
10r2−7r+70=0
Substitute a=10,b=−7 and c=70 into the quadratic formula r=2a−b±b2−4ac
r=2×107±(−7)2−4×10×70
Simplify the expression
r=207±(−7)2−4×10×70
Simplify the expression
More Steps


Evaluate
(−7)2−4×10×70
Multiply the numbers
More Steps


Multiply the terms
4×10×70
Multiply the terms
40×70
Multiply the numbers
2800
(−7)2−2800
Rewrite the expression
72−2800
Evaluate the power
49−2800
Subtract the numbers
−2751
r=207±−2751
Simplify the radical expression
More Steps


Evaluate
−2751
Evaluate the power
2751×−1
Evaluate the power
2751×i
r=207±2751×i
Separate the equation into 2 possible cases
r=207+2751×ir=207−2751×i
Simplify the expression
r=207+202751ir=207−2751×i
Simplify the expression
r=207+202751ir=207−202751i
Solution
r1=207−202751i,r2=207+202751i
Alternative Form
r1≈0.35−2.622499i,r2≈0.35+2.622499i
Show Solution

Rewrite the equation
−1351x2−1351y2=100x4+100y4+4900+200x2y2
Evaluate
710−71r=−72r2×75
Evaluate
More Steps


Evaluate
−72r2×75
Multiply the terms
More Steps


Evaluate
72×75
To multiply the fractions,multiply the numerators and denominators separately
7×72×5
Multiply the numbers
7×710
Multiply the numbers
4910
−4910r2
710−71r=−4910r2
Multiply both sides of the equation by LCD
(710−71r)×49=−4910r2×49
Simplify the equation
More Steps


Evaluate
(710−71r)×49
Apply the distributive property
710×49−71r×49
Simplify
10×7−r×7
Multiply the numbers
70−r×7
Use the commutative property to reorder the terms
70−7r
70−7r=−4910r2×49
Simplify the equation
70−7r=−10r2
Rewrite the expression
−7r+10r2=−70
Use substitution
More Steps


Evaluate
−7r+10r2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
−7r+10(x2+y2)
Simplify the expression
−7r+10x2+10y2
−7r+10x2+10y2=−70
Simplify the expression
−7r=−10x2−10y2−70
Square both sides of the equation
(−7r)2=(−10x2−10y2−70)2
Evaluate
49r2=(−10x2−10y2−70)2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
49(x2+y2)=(−10x2−10y2−70)2
Evaluate the power
49(x2+y2)=(10x2+10y2+70)2
Calculate
49x2+49y2=100x4+100y4+4900+200x2y2+1400x2+1400y2
Move the expression to the left side
49x2+49y2−(1400x2+1400y2)=100x4+100y4+4900+200x2y2
Calculate
More Steps


Evaluate
49x2−1400x2
Collect like terms by calculating the sum or difference of their coefficients
(49−1400)x2
Subtract the numbers
−1351x2
−1351x2+49y2=100x4+100y4+4900+200x2y2+1400y2
Solution
More Steps


Evaluate
49y2−1400y2
Collect like terms by calculating the sum or difference of their coefficients
(49−1400)y2
Subtract the numbers
−1351y2
−1351x2−1351y2=100x4+100y4+4900+200x2y2
Show Solution

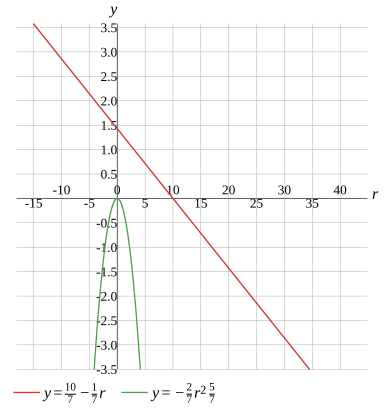
Graph