Solve 10m^6=7m^21

Evaluate

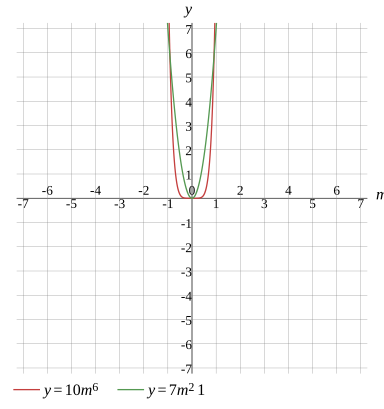
10 m^{6} = 7 m^{2} \times 1

Multiply the terms

10 m^{6} = 7 m^{2}

Add or subtract both sides

10 m^{6} - 7 m^{2} = 0

Factor the expression

m^{2} (10 m^{4} - 7) = 0

Separate the equation into 2 possible cases

m^{2} = 0 10 m^{4} - 7 = 0

The only way a power can be 0 is when the base equals 0

m = 0 10 m^{4} - 7 = 0

Solve the equation

More Steps

m = 0 m = \frac{4 7000}{10} m = - \frac{4 7000}{10}

Solution

m_{1} = - \frac{4 7000}{10}, m_{2} = 0, m_{3} = \frac{4 7000}{10}

Alternative Form

m_{1} \approx - 0.914691, m_{2} = 0, m_{3} \approx 0.914691

Solve the equation