Question
Solve the quadratic equation
Solve by factoring
Solve using the quadratic formula
Solve by completing the square
Load more

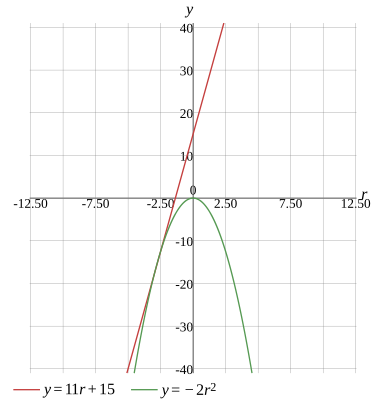
r1=−3,r2=−25
Alternative Form
r1=−3,r2=−2.5
Evaluate
11r+15=−2r2
Swap the sides
−2r2=11r+15
Move the expression to the left side
−2r2−11r−15=0
Factor the expression
More Steps


Evaluate
−2r2−11r−15
Factor out −1 from the expression
−(2r2+11r+15)
Factor the expression
More Steps


Evaluate
2r2+11r+15
Rewrite the expression
2r2+(5+6)r+15
Calculate
2r2+5r+6r+15
Rewrite the expression
r×2r+r×5+3×2r+3×5
Factor out r from the expression
r(2r+5)+3×2r+3×5
Factor out 3 from the expression
r(2r+5)+3(2r+5)
Factor out 2r+5 from the expression
(r+3)(2r+5)
−(r+3)(2r+5)
−(r+3)(2r+5)=0
Divide the terms
(r+3)(2r+5)=0
When the product of factors equals 0,at least one factor is 0
2r+5=0r+3=0
Solve the equation for r
More Steps


Evaluate
2r+5=0
Move the constant to the right-hand side and change its sign
2r=0−5
Removing 0 doesn't change the value,so remove it from the expression
2r=−5
Divide both sides
22r=2−5
Divide the numbers
r=2−5
Use b−a=−ba=−ba to rewrite the fraction
r=−25
r=−25r+3=0
Solve the equation for r
More Steps


Evaluate
r+3=0
Move the constant to the right-hand side and change its sign
r=0−3
Removing 0 doesn't change the value,so remove it from the expression
r=−3
r=−25r=−3
Solution
r1=−3,r2=−25
Alternative Form
r1=−3,r2=−2.5
Show Solution

Rewrite the equation
61x2+61y2=4x4+4y4+225+8x2y2
Evaluate
11r+15=−2r2
Rewrite the expression
11r+2r2=−15
Use substitution
More Steps


Evaluate
11r+2r2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
11r+2(x2+y2)
Simplify the expression
11r+2x2+2y2
11r+2x2+2y2=−15
Simplify the expression
11r=−2x2−2y2−15
Square both sides of the equation
(11r)2=(−2x2−2y2−15)2
Evaluate
121r2=(−2x2−2y2−15)2
To covert the equation to rectangular coordinates using conversion formulas,substitute x2+y2 for r2
121(x2+y2)=(−2x2−2y2−15)2
Evaluate the power
121(x2+y2)=(2x2+2y2+15)2
Calculate
121x2+121y2=4x4+4y4+225+8x2y2+60x2+60y2
Move the expression to the left side
121x2+121y2−(60x2+60y2)=4x4+4y4+225+8x2y2
Calculate
More Steps


Evaluate
121x2−60x2
Collect like terms by calculating the sum or difference of their coefficients
(121−60)x2
Subtract the numbers
61x2
61x2+121y2=4x4+4y4+225+8x2y2+60y2
Solution
More Steps


Evaluate
121y2−60y2
Collect like terms by calculating the sum or difference of their coefficients
(121−60)y2
Subtract the numbers
61y2
61x2+61y2=4x4+4y4+225+8x2y2
Show Solution

Graph