Question
Solve the equation
x1=114104−27118,x2=114104+27118
Alternative Form
x1≈−0.532241,x2≈2.356802
Evaluate
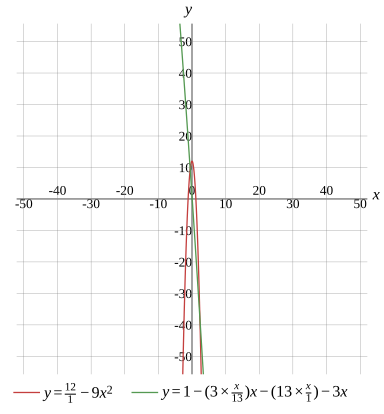
112−9x2=1−(3×13x)x−(13×1x)−3x
Remove the parentheses
112−9x2=1−3×13xx−(13×1x)−3x
Divide the terms
12−9x2=1−3×13xx−(13×1x)−3x
Simplify
More Steps


Evaluate
1−3×13xx−(13×1x)−3x
Divide the terms
1−3×13xx−(13x)−3x
Multiply the terms
1−3×13xx−13x−3x
Multiply the terms
1−133x2−13x−3x
Subtract the terms
More Steps


Evaluate
−13x−3x
Collect like terms by calculating the sum or difference of their coefficients
(−13−3)x
Subtract the numbers
−16x
1−133x2−16x
12−9x2=1−133x2−16x
Multiply both sides of the equation by LCD
(12−9x2)×13=(1−133x2−16x)×13
Simplify the equation
More Steps


Evaluate
(12−9x2)×13
Apply the distributive property
12×13−9x2×13
Multiply the numbers
156−9x2×13
Multiply the numbers
156−117x2
156−117x2=(1−133x2−16x)×13
Simplify the equation
More Steps


Evaluate
(1−133x2−16x)×13
Apply the distributive property
1×13−133x2×13−16x×13
Simplify
1×13−3x2−16x×13
Any expression multiplied by 1 remains the same
13−3x2−16x×13
Multiply the numbers
13−3x2−208x
156−117x2=13−3x2−208x
Move the expression to the left side
156−117x2−(13−3x2−208x)=0
Subtract the terms
More Steps


Evaluate
156−117x2−(13−3x2−208x)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
156−117x2−13+3x2+208x
Subtract the numbers
143−117x2+3x2+208x
Add the terms
More Steps


Evaluate
−117x2+3x2
Collect like terms by calculating the sum or difference of their coefficients
(−117+3)x2
Add the numbers
−114x2
143−114x2+208x
143−114x2+208x=0
Rewrite in standard form
−114x2+208x+143=0
Multiply both sides
114x2−208x−143=0
Substitute a=114,b=−208 and c=−143 into the quadratic formula x=2a−b±b2−4ac
x=2×114208±(−208)2−4×114(−143)
Simplify the expression
x=228208±(−208)2−4×114(−143)
Simplify the expression
More Steps


Evaluate
(−208)2−4×114(−143)
Multiply
More Steps


Multiply the terms
4×114(−143)
Rewrite the expression
−4×114×143
Multiply the terms
−65208
(−208)2−(−65208)
Rewrite the expression
2082−(−65208)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
2082+65208
Evaluate the power
43264+65208
Add the numbers
108472
x=228208±108472
Simplify the radical expression
More Steps


Evaluate
108472
Write the expression as a product where the root of one of the factors can be evaluated
4×27118
Write the number in exponential form with the base of 2
22×27118
The root of a product is equal to the product of the roots of each factor
22×27118
Reduce the index of the radical and exponent with 2
227118
x=228208±227118
Separate the equation into 2 possible cases
x=228208+227118x=228208−227118
Simplify the expression
More Steps


Evaluate
x=228208+227118
Divide the terms
More Steps


Evaluate
228208+227118
Rewrite the expression
2282(104+27118)
Cancel out the common factor 2
114104+27118
x=114104+27118
x=114104+27118x=228208−227118
Simplify the expression
More Steps


Evaluate
x=228208−227118
Divide the terms
More Steps


Evaluate
228208−227118
Rewrite the expression
2282(104−27118)
Cancel out the common factor 2
114104−27118
x=114104−27118
x=114104+27118x=114104−27118
Solution
x1=114104−27118,x2=114104+27118
Alternative Form
x1≈−0.532241,x2≈2.356802
Show Solution

Graph