Solve 15:(x^4)=7 - ScanMath

Question

Solve the equation

x_{1} = - \frac{4 5145}{7}, x_{2} = \frac{4 5145}{7}

Alternative Form

x_{1} \approx - 1.209897, x_{2} \approx 1.209897

Evaluate

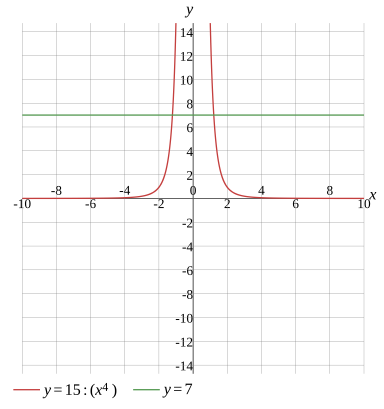
15 \div x^{4} = 7

Find the domain

More Steps

Evaluate

x^{4} \neq = 0

The only way a power can not be 0 is when the base not equals 0

x \neq = 0

15 \div x^{4} = 7, x \neq = 0

Rewrite the expression

\frac{15}{x ^{4}} = 7

Cross multiply

15 = x^{4} \times 7

Simplify the equation

15 = 7 x^{4}

Swap the sides of the equation

7 x^{4} = 15

Divide both sides

\frac{7 x ^{4}}{7} = \frac{15}{7}

Divide the numbers

x^{4} = \frac{15}{7}

Take the root of both sides of the equation and remember to use both positive and negative roots

x = \pm 4 \frac{15}{7}

Simplify the expression

More Steps

Evaluate

4 \frac{15}{7}

To take a root of a fraction,take the root of the numerator and denominator separately

\frac{4 15}{4 7}

Multiply by the Conjugate

\frac{4 15 \times 4 7 ^{3}}{4 7 \times 4 7 ^{3}}

Simplify

\frac{4 15 \times 4 343}{4 7 \times 4 7 ^{3}}

Multiply the numbers

More Steps

Evaluate

415 \times 4343

The product of roots with the same index is equal to the root of the product

4 15 \times 343

Calculate the product

45145

\frac{4 5145}{4 7 \times 4 7 ^{3}}

Multiply the numbers

More Steps

Evaluate

47 \times 4 7^{3}

The product of roots with the same index is equal to the root of the product

4 7 \times 7^{3}

Calculate the product

4 7^{4}

Reduce the index of the radical and exponent with 4

7

\frac{4 5145}{7}

x = \pm \frac{4 5145}{7}

Separate the equation into 2 possible cases

x = \frac{4 5145}{7} x = - \frac{4 5145}{7}

Check if the solution is in the defined range

x = \frac{4 5145}{7} x = - \frac{4 5145}{7}, x \neq = 0

Find the intersection of the solution and the defined range

x = \frac{4 5145}{7} x = - \frac{4 5145}{7}

Solution

x_{1} = - \frac{4 5145}{7}, x_{2} = \frac{4 5145}{7}

Alternative Form

x_{1} \approx - 1.209897, x_{2} \approx 1.209897

Show Solution