Question
Solve the equation
θ={18π+32kπ185π+32kπ,k∈Z
Alternative Form
θ={10∘+120∘k50∘+120∘k,k∈Z
Alternative Form
θ≈{0.174533+32kπ0.872665+32kπ,k∈Z
Evaluate
2sin(3θ)−1=0
Move the constant to the right-hand side and change its sign
2sin(3θ)=0+1
Removing 0 doesn't change the value,so remove it from the expression
2sin(3θ)=1
Divide both sides
22sin(3θ)=21
Divide the numbers
sin(3θ)=21
Use the inverse trigonometric function
3θ=arcsin(21)
Calculate
3θ=6π3θ=65π
Add the period of 2kπ,k∈Z to find all solutions
3θ=6π+2kπ,k∈Z3θ=65π+2kπ,k∈Z
Calculate
More Steps


Evaluate
3θ=6π+2kπ
Divide both sides
33θ=36π+2kπ
Divide the numbers
θ=36π+2kπ
Divide the numbers
θ=18π+32kπ
θ=18π+32kπ,k∈Z3θ=65π+2kπ,k∈Z
Calculate
More Steps


Evaluate
3θ=65π+2kπ
Divide both sides
33θ=365π+2kπ
Divide the numbers
θ=365π+2kπ
Divide the numbers
θ=185π+32kπ
θ=18π+32kπ,k∈Zθ=185π+32kπ,k∈Z
Solution
θ={18π+32kπ185π+32kπ,k∈Z
Alternative Form
θ={10∘+120∘k50∘+120∘k,k∈Z
Alternative Form
θ≈{0.174533+32kπ0.872665+32kπ,k∈Z
Show Solution

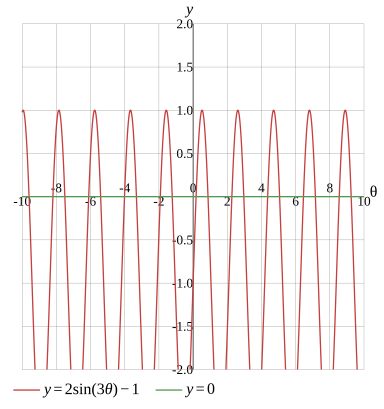
Graph