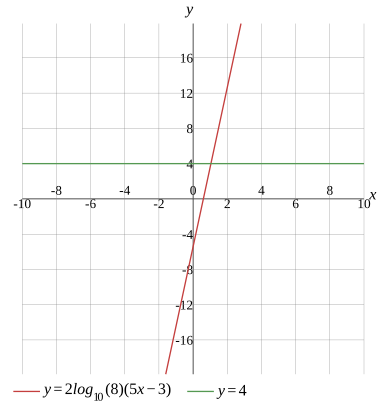
Question
Solve the equation
x=1511+2log2(5)
Alternative Form
x≈1.042924
Evaluate
2log10(8)×(5x−3)=4
Divide both sides
2log10(8)2log10(8)×(5x−3)=2log10(8)4
Divide the numbers
5x−3=2log10(8)4
Cancel out the common factor 2
5x−3=log10(8)2
Move the constant to the right side
5x=log10(8)2+3
Add the numbers
More Steps


Evaluate
log10(8)2+3
Simplify
More Steps


Evaluate
log10(8)
Write the number in exponential form with the base of 2
log10(23)
Calculate
3log10(2)
3log10(2)2+3
Reduce fractions to a common denominator
3log10(2)2+3log10(2)3×3log10(2)
Write all numerators above the common denominator
3log10(2)2+3×3log10(2)
Multiply the terms
3log10(2)2+9log10(2)
Rewrite in terms of common logarithms
More Steps


Evaluate the logarithm
2+9log10(2)
Rewrite in terms of common logarithms
log10(100)+9log10(2)
Calculate
log10(100)+log10(29)
Use the logarithm product rule
log10(100×29)
Evaluate the logarithm
log10(51200)
3log10(2)log10(51200)
Rewrite in terms of common logarithms
log10(23)log10(51200)
Use the logarithm base change rule
log23(51200)
5x=log23(51200)
Divide both sides
55x=5log23(51200)
Divide the numbers
x=5log23(51200)
Simplify
More Steps


Evaluate
5log23(51200)
Use logamb=m1logab to simplify the expression
531log2(51200)
Rewrite the expression
53log2(51200)
Multiply by the reciprocal
3log2(51200)×51
To multiply the fractions,multiply the numerators and denominators separately
3×5log2(51200)
Multiply the numbers
15log2(51200)
x=15log2(51200)
Solution
x=1511+2log2(5)
Alternative Form
x≈1.042924
Show Solution

Graph