Solve 2loga (a^3a) = loga (a-30)

Evaluate

2 lo g_{10} (a) \times (a^{3} \times a) = lo g_{10} (a) \times (a - 30)

Find the domain

2 lo g_{10} (a) \times (a^{3} \times a) = lo g_{10} (a) \times (a - 30), a > 0

Remove the parentheses

2 lo g_{10} (a) \times a^{3} \times a = lo g_{10} (a) \times (a - 30)

Multiply

More Steps

2 lo g_{10} (a) \times a^{4} = lo g_{10} (a) \times (a - 30)

Multiply the terms

2 lo g_{10} (a) \times a^{4} = (a - 30) \times lo g_{10} (a)

Calculate

2 lo g_{10} (a) \times a^{4} = a lo g_{10} (a) - 30 lo g_{10} (a)

Move the expression to the left side

2 lo g_{10} (a) \times a^{4} - (a lo g_{10} (a) - 30 lo g_{10} (a)) = 0

If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses

2 lo g_{10} (a) \times a^{4} - a lo g_{10} (a) + 30 lo g_{10} (a) = 0

Factor the expression

lo g_{10} (a) \times (2 a^{4} - a + 30) = 0

Separate the equation into 2 possible cases

lo g_{10} (a) = 0 2 a^{4} - a + 30 = 0

Solve the equation

More Steps

a = 1 2 a^{4} - a + 30 = 0

Solve the equation

a = 1 a \in / R

Find the union

a = 1

Check if the solution is in the defined range

a = 1, a > 0

Solution

a = 1

Solve the equation

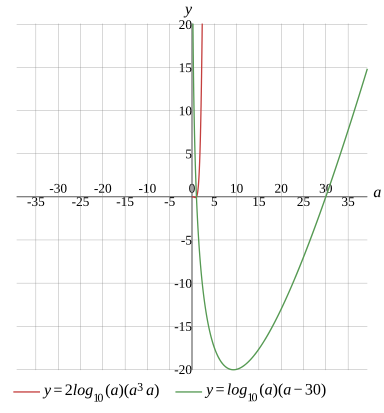
Graph