Question
Function
Find the x-intercept/zero
Find the y-intercept
Find the slope
x=811
Evaluate
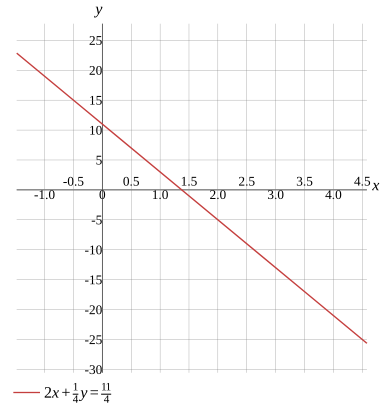
2x+41y=411
To find the x-intercept,set y=0
2x+41×0=411
Any expression multiplied by 0 equals 0
2x+0=411
Removing 0 doesn't change the value,so remove it from the expression
2x=411
Multiply by the reciprocal
2x×21=411×21
Multiply
x=411×21
Solution
More Steps


Evaluate
411×21
To multiply the fractions,multiply the numerators and denominators separately
4×211
Multiply the numbers
811
x=811
Show Solution

Solve the equation
Solve for x
Solve for y
x=811−y
Evaluate
2x+41y=411
Move the expression to the right-hand side and change its sign
2x=411−41y
Divide both sides
22x=2411−41y
Divide the numbers
x=2411−41y
Solution
More Steps


Evaluate
2411−41y
Rewrite the expression
2411−y
Multiply by the reciprocal
411−y×21
To multiply the fractions,multiply the numerators and denominators separately
4×211−y
Multiply the numbers
811−y
x=811−y
Show Solution

Testing for symmetry
Testing for symmetry about the origin
Testing for symmetry about the x-axis
Testing for symmetry about the y-axis
Not symmetry with respect to the origin
Evaluate
2x+41⋅y=411
To test if the graph of 2x+41y=411 is symmetry with respect to the origin,substitute -x for x and -y for y
2(−x)+41(−y)=411
Evaluate
More Steps


Evaluate
2(−x)+41(−y)
Multiply the numbers
−2x+41(−y)
Multiplying or dividing an odd number of negative terms equals a negative
−2x−41y
−2x−41y=411
Solution
Not symmetry with respect to the origin
Show Solution

Rewrite the equation
Rewrite in polar form
Rewrite in standard form
Rewrite in slope-intercept form
r=8cos(θ)+sin(θ)11
Evaluate
2x+41y=411
Multiply both sides of the equation by LCD
(2x+41y)×4=411×4
Simplify the equation
More Steps


Evaluate
(2x+41y)×4
Apply the distributive property
2x×4+41y×4
Simplify
2x×4+y
Multiply the numbers
8x+y
8x+y=411×4
Simplify the equation
8x+y=11
To convert the equation to polar coordinates,substitute x for rcos(θ) and y for rsin(θ)
8cos(θ)×r+sin(θ)×r=11
Factor the expression
(8cos(θ)+sin(θ))r=11
Solution
r=8cos(θ)+sin(θ)11
Show Solution

Find the first derivative
Find the derivative with respect to x
Find the derivative with respect to y
dxdy=−8
Calculate
2x+41⋅y=411
Take the derivative of both sides
dxd(2x+41y)=dxd(411)
Calculate the derivative
More Steps


Evaluate
dxd(2x+41y)
Use differentiation rules
dxd(2x)+dxd(41y)
Evaluate the derivative
More Steps


Evaluate
dxd(2x)
Use differentiation rule dxd(cf(x))=c×dxd(f(x))
2×dxd(x)
Use dxdxn=nxn−1 to find derivative
2×1
Any expression multiplied by 1 remains the same
2
2+dxd(41y)
Evaluate the derivative
More Steps


Evaluate
dxd(41y)
Use differentiation rules
dyd(41y)×dxdy
Evaluate the derivative
41dxdy
2+41dxdy
2+41dxdy=dxd(411)
Calculate the derivative
2+41dxdy=0
Move the constant to the right-hand side and change its sign
41dxdy=0−2
Removing 0 doesn't change the value,so remove it from the expression
41dxdy=−2
Multiply by the reciprocal
41dxdy×4=−2×4
Multiply
dxdy=−2×4
Solution
dxdy=−8
Show Solution

Find the second derivative
Find the second derivative with respect to x
Find the second derivative with respect to y
dx2d2y=0
Calculate
2x+41⋅y=411
Take the derivative of both sides
dxd(2x+41y)=dxd(411)
Calculate the derivative
More Steps


Evaluate
dxd(2x+41y)
Use differentiation rules
dxd(2x)+dxd(41y)
Evaluate the derivative
More Steps


Evaluate
dxd(2x)
Use differentiation rule dxd(cf(x))=c×dxd(f(x))
2×dxd(x)
Use dxdxn=nxn−1 to find derivative
2×1
Any expression multiplied by 1 remains the same
2
2+dxd(41y)
Evaluate the derivative
More Steps


Evaluate
dxd(41y)
Use differentiation rules
dyd(41y)×dxdy
Evaluate the derivative
41dxdy
2+41dxdy
2+41dxdy=dxd(411)
Calculate the derivative
2+41dxdy=0
Move the constant to the right-hand side and change its sign
41dxdy=0−2
Removing 0 doesn't change the value,so remove it from the expression
41dxdy=−2
Multiply by the reciprocal
41dxdy×4=−2×4
Multiply
dxdy=−2×4
Multiply
dxdy=−8
Take the derivative of both sides
dxd(dxdy)=dxd(−8)
Calculate the derivative
dx2d2y=dxd(−8)
Solution
dx2d2y=0
Show Solution

Graph