Question
Solve the equation
x∈/R
Alternative Form
No real solution
Evaluate
(2×xx)−42x−x5−3=325
Simplify
More Steps


Evaluate
(2×xx)−42x−x5−3
Divide the terms
(2×1)−42x−x5−3
Any expression multiplied by 1 remains the same
2−42x−x5−3
Subtract the numbers
−1−42x−x5
−1−42x−x5=325
Multiply both sides of the equation by LCD
(−1−42x−x5)×3x=325×3x
Simplify the equation
More Steps


Evaluate
(−1−42x−x5)×3x
Apply the distributive property
−3x−42x×3x−x5×3x
Simplify
−3x−42x×3x−5×3
Multiply the terms
More Steps


Evaluate
−42x×3x
Multiply the numbers
−126x×x
Multiply the terms
−126x2
−3x−126x2−5×3
Multiply the numbers
−3x−126x2−15
−3x−126x2−15=325×3x
Simplify the equation
−3x−126x2−15=25x
Move the expression to the left side
−3x−126x2−15−25x=0
Subtract the terms
More Steps


Evaluate
−3x−25x
Collect like terms by calculating the sum or difference of their coefficients
(−3−25)x
Subtract the numbers
−28x
−28x−126x2−15=0
Rewrite in standard form
−126x2−28x−15=0
Multiply both sides
126x2+28x+15=0
Substitute a=126,b=28 and c=15 into the quadratic formula x=2a−b±b2−4ac
x=2×126−28±282−4×126×15
Simplify the expression
x=252−28±282−4×126×15
Simplify the expression
More Steps


Evaluate
282−4×126×15
Multiply the terms
More Steps


Multiply the terms
4×126×15
Multiply the terms
504×15
Multiply the numbers
7560
282−7560
Evaluate the power
784−7560
Subtract the numbers
−6776
x=252−28±−6776
Solution
x∈/R
Alternative Form
No real solution
Show Solution

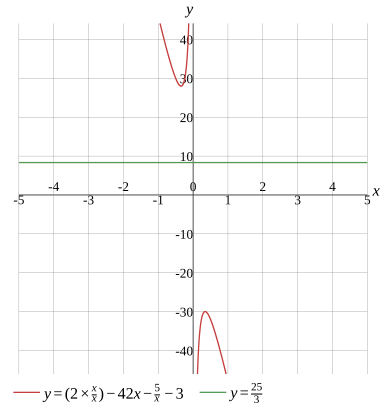
Graph