Solve 2x=3y 8 x=2y - ScanMath

HOME CALCULATOR

DOWNLOAD FOR FREE

Algebra
Calculus
Trigonometry
Matrix

Type your math problem... 2x=3y 8 x=2y

Question

Solve the system of equations

Solve using the substitution method

solver-selected-icon

Solve using the elimination method

(x_{1}, y_{1}) = (0, 0) (x_{2}, y_{2}) = (\frac{1}{12}, \frac{1}{12})

Evaluate

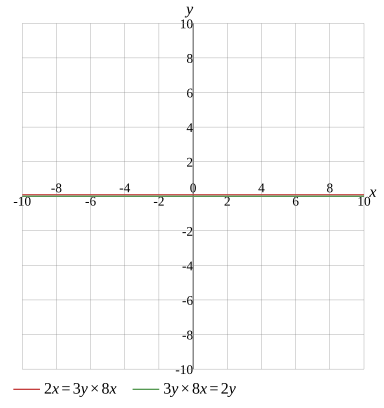
{2 x = 3 y \times 8 x 3 y \times 8 x = 2 y

Calculate

{2 x = 24 y x 3 y \times 8 x = 2 y

Calculate

{2 x = 24 y x 24 y x = 2 y

Solve the equation

More Steps

{x = 0 \cup y = \frac{1}{12} 24 y x = 2 y

Evaluate

{x = 0 24 y x = 2 y \cup {y = \frac{1}{12} 24 y x = 2 y

Calculate

More Steps

{x = 0 y = 0 \cup {y = \frac{1}{12} 24 y x = 2 y

Calculate

More Steps

{x = 0 y = 0 \cup {x = \frac{1}{12} y = \frac{1}{12}

Check the solution

More Steps

{x = 0 y = 0 \cup {x = \frac{1}{12} y = \frac{1}{12}

Check the solution

More Steps

{x = 0 y = 0 \cup {x = \frac{1}{12} y = \frac{1}{12}

Solution

(x_{1}, y_{1}) = (0, 0) (x_{2}, y_{2}) = (\frac{1}{12}, \frac{1}{12})

Show Solution

Graph

Graph