Question
Solve the equation(The real numbers system)
x∈/R
Alternative Form
No real solution
Evaluate
2x2×9=6x−9
Multiply the terms
18x2=6x−9
Move the expression to the left side
18x2−6x+9=0
Substitute a=18,b=−6 and c=9 into the quadratic formula x=2a−b±b2−4ac
x=2×186±(−6)2−4×18×9
Simplify the expression
x=366±(−6)2−4×18×9
Simplify the expression
More Steps


Evaluate
(−6)2−4×18×9
Multiply the terms
More Steps


Multiply the terms
4×18×9
Multiply the terms
72×9
Multiply the numbers
648
(−6)2−648
Rewrite the expression
62−648
Evaluate the power
36−648
Subtract the numbers
−612
x=366±−612
Solution
x∈/R
Alternative Form
No real solution
Show Solution

Solve the equation(The complex numbers system)
Solve using the quadratic formula in the complex numbers system
Solve by completing the square in the complex numbers system
Solve using the PQ formula in the complex numbers system
x1=61−617i,x2=61+617i
Alternative Form
x1≈0.16˙−0.687184i,x2≈0.16˙+0.687184i
Evaluate
2x2×9=6x−9
Multiply the terms
18x2=6x−9
Move the expression to the left side
18x2−6x+9=0
Substitute a=18,b=−6 and c=9 into the quadratic formula x=2a−b±b2−4ac
x=2×186±(−6)2−4×18×9
Simplify the expression
x=366±(−6)2−4×18×9
Simplify the expression
More Steps


Evaluate
(−6)2−4×18×9
Multiply the terms
More Steps


Multiply the terms
4×18×9
Multiply the terms
72×9
Multiply the numbers
648
(−6)2−648
Rewrite the expression
62−648
Evaluate the power
36−648
Subtract the numbers
−612
x=366±−612
Simplify the radical expression
More Steps


Evaluate
−612
Evaluate the power
612×−1
Evaluate the power
612×i
Evaluate the power
More Steps


Evaluate
612
Write the expression as a product where the root of one of the factors can be evaluated
36×17
Write the number in exponential form with the base of 6
62×17
The root of a product is equal to the product of the roots of each factor
62×17
Reduce the index of the radical and exponent with 2
617
617×i
x=366±617×i
Separate the equation into 2 possible cases
x=366+617×ix=366−617×i
Simplify the expression
More Steps


Evaluate
x=366+617×i
Divide the terms
More Steps


Evaluate
366+617×i
Rewrite the expression
366(1+17×i)
Cancel out the common factor 6
61+17×i
Simplify
61+617i
x=61+617i
x=61+617ix=366−617×i
Simplify the expression
More Steps


Evaluate
x=366−617×i
Divide the terms
More Steps


Evaluate
366−617×i
Rewrite the expression
366(1−17×i)
Cancel out the common factor 6
61−17×i
Simplify
61−617i
x=61−617i
x=61+617ix=61−617i
Solution
x1=61−617i,x2=61+617i
Alternative Form
x1≈0.16˙−0.687184i,x2≈0.16˙+0.687184i
Show Solution

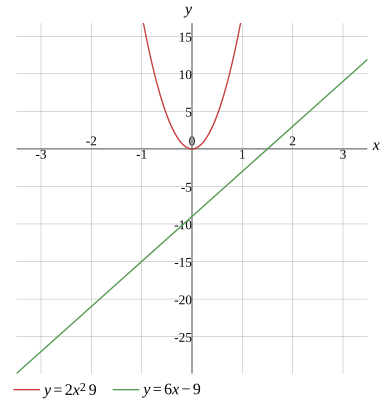
Graph