Question
Solve the inequality
Solve for x
Solve for y
x>−∣y∣43y3,y>0∩x<∣y∣43y3,y>0∪x>∣y∣43y3,y<0∪x<−∣y∣43y3,y<0∪x>−∣y∣43y3,y>0∩x<∣y∣43y3,y>0
Evaluate
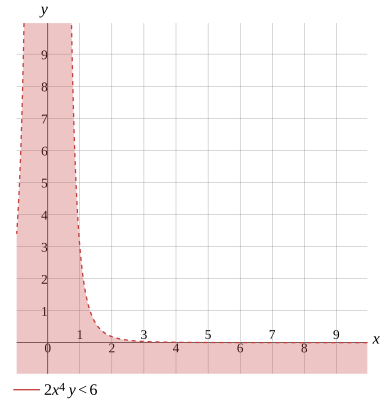
2x4y<6
Rewrite the expression
2yx4<6
Divide both sides
2y2yx4<2y6
Divide the numbers
x4<2y6
Cancel out the common factor 2
x4<y3
Rewrite the inequalities
{x4<y3y>0{x4>y3y<0
Calculate
More Steps


Calculate
x4<y3
Take the 4-th root on both sides of the inequality
4x4<4y3
Calculate
∣x∣<∣y∣43y3
Separate the inequality into 2 possible cases
⎩⎨⎧x<∣y∣43y3x>−∣y∣43y3
Find the intersection
x<∣y∣43y3∩x>−∣y∣43y3
{x<∣y∣43y3∩x>−∣y∣43y3y>0{x4>y3y<0
Calculate
More Steps


Calculate
x4>y3
Take the 4-th root on both sides of the inequality
4x4>4y3
Calculate
∣x∣>∣y∣43y3
Separate the inequality into 2 possible cases
x>∣y∣43y3x<−∣y∣43y3
{x<∣y∣43y3∩x>−∣y∣43y3y>0⎩⎨⎧x>∣y∣43y3x<−∣y∣43y3y<0
Calculate
{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0⎩⎨⎧x>∣y∣43y3x<−∣y∣43y3y<0
Calculate
{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0{x>∣y∣43y3y<0{x<−∣y∣43y3y<0
Rearrange the terms
{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0∪{x>∣y∣43y3y<0∪{x<−∣y∣43y3y<0∪{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0
Check if the solution is in the defined range
{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0∪{x>∣y∣43y3y<0∪{x<−∣y∣43y3y<0∪{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0,y=0
Find the intersection of the solution and the defined range
{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0∪{x>∣y∣43y3y<0∪{x<−∣y∣43y3y<0∪{x>−∣y∣43y3y>0∩{x<∣y∣43y3y>0
Solution
x>−∣y∣43y3,y>0∩x<∣y∣43y3,y>0∪x>∣y∣43y3,y<0∪x<−∣y∣43y3,y<0∪x>−∣y∣43y3,y>0∩x<∣y∣43y3,y>0
Show Solution

Graph