Solve 3 log 9 ( 5 x - 5 ) = 5

Question

Solve the equation

x = \frac{6 + lo g _{3} ( 10 )}{6}

Alternative Form

x \approx 1.349317

Evaluate

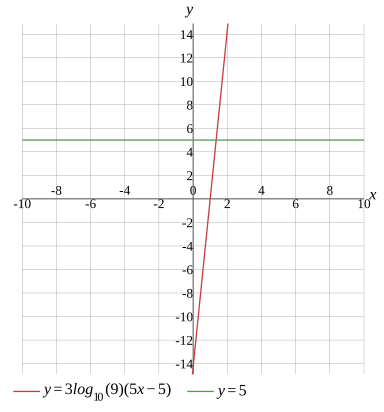
3 lo g_{10} (9) \times (5 x - 5) = 5

Divide both sides

\frac{3 lo g _{10} ( 9 ) \times ( 5 x - 5 )}{3 lo g _{10} ( 9 )} = \frac{5}{3 lo g _{10} ( 9 )}

Divide the numbers

5 x - 5 = \frac{5}{3 lo g _{10} ( 9 )}

Move the constant to the right side

5 x = \frac{5}{3 lo g _{10} ( 9 )} + 5

Add the numbers

More Steps

5 x = \frac{5}{6} lo g_{3} (7290)

Divide both sides

\frac{5 x}{5} = \frac{\frac{5}{6} lo g _{3} ( 7290 )}{5}

Divide the numbers

x = \frac{\frac{5}{6} lo g _{3} ( 7290 )}{5}

Divide the numbers

More Steps

x = \frac{lo g _{3} ( 7290 )}{6}

Solution

More Steps

x = \frac{6 + lo g _{3} ( 10 )}{6}

Alternative Form

x \approx 1.349317

Show Solution