Solve 3( 32(2t-1) ) 2 -2(2t-1)( 32(2t-1) ) t^2 =0

Question

Solve the equation

t_{1} = \frac{1}{2}, t_{2} \approx 1.337944

Alternative Form

t_{1} = 0.5, t_{2} \approx 1.337944

Evaluate

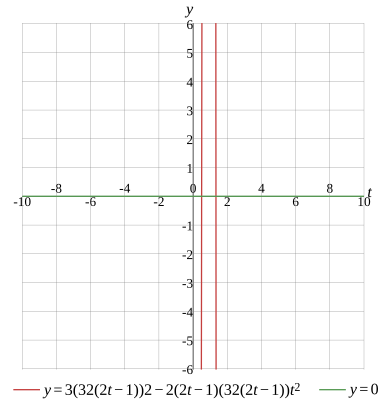
3 (32 (2 t - 1)) \times 2 - 2 (2 t - 1) (32 (2 t - 1)) t^{2} = 0

Remove the parentheses

3 \times 32 (2 t - 1) \times 2 - 2 (2 t - 1) \times 32 (2 t - 1) t^{2} = 0

Simplify

More Steps

192 (2 t - 1) - 64 t^{2} (2 t - 1)^{2} = 0

Calculate

More Steps

384 t - 192 - 256 t^{4} + 256 t^{3} - 64 t^{2} = 0

Factor the expression

- 64 (1 - 2 t) (3 - 2 t^{3} + t^{2}) = 0

Divide both sides

(1 - 2 t) (3 - 2 t^{3} + t^{2}) = 0

Separate the equation into 2 possible cases

1 - 2 t = 0 3 - 2 t^{3} + t^{2} = 0

Solve the equation

More Steps

t = \frac{1}{2} 3 - 2 t^{3} + t^{2} = 0

Solve the equation

t = \frac{1}{2} t \approx 1.337944

Solution

t_{1} = \frac{1}{2}, t_{2} \approx 1.337944

Alternative Form

t_{1} = 0.5, t_{2} \approx 1.337944

Show Solution