Algebra
Calculus
Trigonometry
Matrix
Question
Solve the equation
x=0
Evaluate
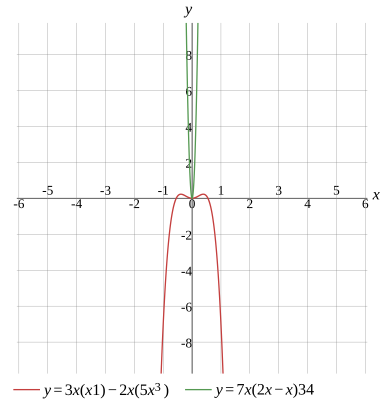
3x(x×1)−2x×5x3=7x(2x−x)×34
Remove the parentheses
3x×x×1−2x×5x3=7x(2x−x)×34
Simplify
More Steps
Evaluate
3x×x×1−2x×5x3
Multiply the terms
More Steps
Multiply the terms
3x×x×1
Rewrite the expression
3x×x
Multiply the terms
3x2
3x2−2x×5x3
Multiply
More Steps
Multiply the terms
2x×5x3
Multiply the terms
10x×x3
Multiply the terms with the same base by adding their exponents
10x1+3
Add the numbers
10x4
3x2−10x4
3x2−10x4=7x(2x−x)×34
Simplify
More Steps
Evaluate
7x(2x−x)×34
Subtract the terms
More Steps
Simplify
2x−x
Collect like terms by calculating the sum or difference of their coefficients
(2−1)x
Subtract the numbers
x
7x×x×34
Multiply the terms
238x×x
Multiply the terms
238x2
3x2−10x4=238x2
Move the expression to the left side
3x2−10x4−238x2=0
Subtract the terms
More Steps
Evaluate
3x2−238x2
Collect like terms by calculating the sum or difference of their coefficients
(3−238)x2
Subtract the numbers
−235x2
−235x2−10x4=0
The statement is true only the each term equals to 0
{−235x2=0−10x4=0
Calculate
More Steps
Evaluate
−235x2=0
Change the signs on both sides of the equation
235x2=0
Rewrite the expression
x2=0
The only way a power can be 0 is when the base equals 0
x=0
{x=0−10x4=0
Calculate
More Steps
Evaluate
−10x4=0
Change the signs on both sides of the equation
10x4=0
Rewrite the expression
x4=0
The only way a power can be 0 is when the base equals 0
x=0
{x=0x=0
Solution
x=0
Show Solution
Graph
