Solve 3x-2-4y=0 - ScanMath

Question

Function

Find the x -intercept/zero

Find the y-intercept

Find the slope

x = \frac{2}{3}

Evaluate

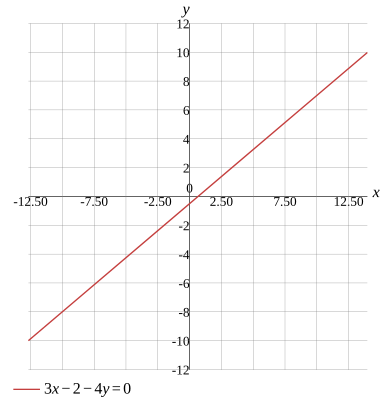
3 x - 2 - 4 y = 0

To find the x -intercept,set y =0

3 x - 2 - 4 \times 0 = 0

Any expression multiplied by 0 equals 0

3 x - 2 - 0 = 0

Removing 0 doesn't change the value,so remove it from the expression

3 x - 2 = 0

Move the constant to the right-hand side and change its sign

3 x = 0 + 2

Removing 0 doesn't change the value,so remove it from the expression

3 x = 2

Divide both sides

\frac{3 x}{3} = \frac{2}{3}

Solution

x = \frac{2}{3}

Show Solution

Solve the equation

Solve for x

Solve for y

x = \frac{2 + 4 y}{3}

Evaluate

3 x - 2 - 4 y = 0

Move the expression to the right-hand side and change its sign

3 x = 0 + 2 + 4 y

Removing 0 doesn't change the value,so remove it from the expression

3 x = 2 + 4 y

Divide both sides

\frac{3 x}{3} = \frac{2 + 4 y}{3}

Solution

x = \frac{2 + 4 y}{3}

Show Solution

Testing for symmetry

Testing for symmetry about the origin

Testing for symmetry about the x-axis

Testing for symmetry about the y-axis

Not symmetry with respect to the origin

Evaluate

3 x - 2 - 4 y = 0

To test if the graph of 3 x - 2 - 4 y = 0 is symmetry with respect to the origin,substitute -x for x and -y for y

3 (- x) - 2 - 4 (- y) = 0

Evaluate

More Steps

Evaluate

3 (- x) - 2 - 4 (- y)

Multiply the numbers

- 3 x - 2 - 4 (- y)

Multiply the numbers

- 3 x - 2 + 4 y

- 3 x - 2 + 4 y = 0

Solution

Not symmetry with respect to the origin

Show Solution

Rewrite the equation

Rewrite in polar form

Rewrite in standard form

Rewrite in slope-intercept form

r = \frac{2}{3 cos ( θ ) - 4 sin ( θ )}

Evaluate

3 x - 2 - 4 y = 0

To convert the equation to polar coordinates,substitute x for r cos (θ) and y for r sin (θ)

3 cos (θ) \times r - 2 - 4 sin (θ) \times r = 0

Factor the expression

(3 cos (θ) - 4 sin (θ)) r - 2 = 0

Subtract the terms

(3 cos (θ) - 4 sin (θ)) r - 2 - (- 2) = 0 - (- 2)

Evaluate

(3 cos (θ) - 4 sin (θ)) r = 2

Solution

r = \frac{2}{3 cos ( θ ) - 4 sin ( θ )}

Show Solution

Find the first derivative

Find the derivative with respect to x

Find the derivative with respect to y

\frac{d y}{d x} = \frac{3}{4}

Calculate

3 x - 2 - 4 y = 0

Take the derivative of both sides

\frac{d}{d x} (3 x - 2 - 4 y) = \frac{d}{d x} (0)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (3 x - 2 - 4 y)

Use differentiation rules

\frac{d}{d x} (3 x) + \frac{d}{d x} (- 2) + \frac{d}{d x} (- 4 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (3 x)

Use differentiation rule \frac{d}{d x} (c f (x)) = c \times \frac{d}{d x} (f (x))

3 \times \frac{d}{d x} (x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

3 \times 1

Any expression multiplied by 1 remains the same

3

3 + \frac{d}{d x} (- 2) + \frac{d}{d x} (- 4 y)

Use \frac{d}{d x} (c) = 0 to find derivative

3 + 0 + \frac{d}{d x} (- 4 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (- 4 y)

Use differentiation rules

\frac{d}{d y} (- 4 y) \times \frac{d y}{d x}

Evaluate the derivative

- 4 \frac{d y}{d x}

3 + 0 - 4 \frac{d y}{d x}

Evaluate

3 - 4 \frac{d y}{d x}

3 - 4 \frac{d y}{d x} = \frac{d}{d x} (0)

Calculate the derivative

3 - 4 \frac{d y}{d x} = 0

Move the constant to the right-hand side and change its sign

- 4 \frac{d y}{d x} = 0 - 3

Removing 0 doesn't change the value,so remove it from the expression

- 4 \frac{d y}{d x} = - 3

Change the signs on both sides of the equation

4 \frac{d y}{d x} = 3

Divide both sides

\frac{4 \frac{d y}{d x}}{4} = \frac{3}{4}

Solution

\frac{d y}{d x} = \frac{3}{4}

Show Solution

Find the second derivative

Find the second derivative with respect to x

Find the second derivative with respect to y

\frac{d ^{2} y}{d x ^{2}} = 0

Calculate

3 x - 2 - 4 y = 0

Take the derivative of both sides

\frac{d}{d x} (3 x - 2 - 4 y) = \frac{d}{d x} (0)

Calculate the derivative

More Steps

Evaluate

\frac{d}{d x} (3 x - 2 - 4 y)

Use differentiation rules

\frac{d}{d x} (3 x) + \frac{d}{d x} (- 2) + \frac{d}{d x} (- 4 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (3 x)

Use differentiation rule \frac{d}{d x} (c f (x)) = c \times \frac{d}{d x} (f (x))

3 \times \frac{d}{d x} (x)

Use \frac{d}{d x} x^{n} = n x^{n - 1} to find derivative

3 \times 1

Any expression multiplied by 1 remains the same

3

3 + \frac{d}{d x} (- 2) + \frac{d}{d x} (- 4 y)

Use \frac{d}{d x} (c) = 0 to find derivative

3 + 0 + \frac{d}{d x} (- 4 y)

Evaluate the derivative

More Steps

Evaluate

\frac{d}{d x} (- 4 y)

Use differentiation rules

\frac{d}{d y} (- 4 y) \times \frac{d y}{d x}

Evaluate the derivative

- 4 \frac{d y}{d x}

3 + 0 - 4 \frac{d y}{d x}

Evaluate

3 - 4 \frac{d y}{d x}

3 - 4 \frac{d y}{d x} = \frac{d}{d x} (0)

Calculate the derivative

3 - 4 \frac{d y}{d x} = 0

Move the constant to the right-hand side and change its sign

- 4 \frac{d y}{d x} = 0 - 3

Removing 0 doesn't change the value,so remove it from the expression

- 4 \frac{d y}{d x} = - 3

Change the signs on both sides of the equation

4 \frac{d y}{d x} = 3

Divide both sides

\frac{4 \frac{d y}{d x}}{4} = \frac{3}{4}

Divide the numbers

\frac{d y}{d x} = \frac{3}{4}

Take the derivative of both sides

\frac{d}{d x} (\frac{d y}{d x}) = \frac{d}{d x} (\frac{3}{4})

Calculate the derivative

\frac{d ^{2} y}{d x ^{2}} = \frac{d}{d x} (\frac{3}{4})

Solution

\frac{d ^{2} y}{d x ^{2}} = 0

Show Solution

Function

Solve the equation

Testing for symmetry

Rewrite the equation

Find the first derivative

Find the second derivative

Graph