Algebra
Calculus
Trigonometry
Matrix
Question
Solve the quadratic equation
Solve using the quadratic formula
Solve by completing the square
Solve using the PQ formula
w1=3−7,w2=3+7
Alternative Form
w1≈0.354249,w2≈5.645751
Evaluate
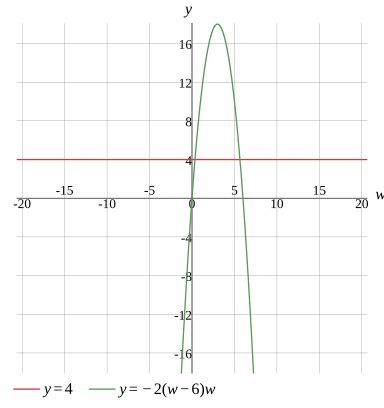
4=−2(w−6)w
Multiply the terms
4=−2w(w−6)
Swap the sides
−2w(w−6)=4
Expand the expression
More Steps
Evaluate
−2w(w−6)
Apply the distributive property
−2w×w−(−2w×6)
Multiply the terms
−2w2−(−2w×6)
Multiply the numbers
−2w2−(−12w)
If a negative sign or a subtraction symbol appears outside parentheses, remove the parentheses and change the sign of every term within the parentheses
−2w2+12w
−2w2+12w=4
Move the expression to the left side
−2w2+12w−4=0
Multiply both sides
2w2−12w+4=0
Substitute a=2,b=−12 and c=4 into the quadratic formula w=2a−b±b2−4ac
w=2×212±(−12)2−4×2×4
Simplify the expression
w=412±(−12)2−4×2×4
Simplify the expression
More Steps
Evaluate
(−12)2−4×2×4
Multiply the terms
More Steps
Multiply the terms
4×2×4
Multiply the terms
8×4
Multiply the numbers
32
(−12)2−32
Rewrite the expression
122−32
Evaluate the power
144−32
Subtract the numbers
112
w=412±112
Simplify the radical expression
More Steps
Evaluate
112
Write the expression as a product where the root of one of the factors can be evaluated
16×7
Write the number in exponential form with the base of 4
42×7
The root of a product is equal to the product of the roots of each factor
42×7
Reduce the index of the radical and exponent with 2
47
w=412±47
Separate the equation into 2 possible cases
w=412+47w=412−47
Simplify the expression
More Steps
Evaluate
w=412+47
Divide the terms
More Steps
Evaluate
412+47
Rewrite the expression
44(3+7)
Reduce the fraction
3+7
w=3+7
w=3+7w=412−47
Simplify the expression
More Steps
Evaluate
w=412−47
Divide the terms
More Steps
Evaluate
412−47
Rewrite the expression
44(3−7)
Reduce the fraction
3−7
w=3−7
w=3+7w=3−7
Solution
w1=3−7,w2=3+7
Alternative Form
w1≈0.354249,w2≈5.645751
Show Solution
Graph
